Функции REG_x (y) и REG_y (x)

Чтобы открыть функциональную клавиатуру, нажмите ссылку f (x) , которая находится в редакторе уравнений, когда мы позиционируем себя на ней.

В нижней части функциональной клавиатуры есть две кнопки интерполяции, которые позволяют получить результаты линейной интерполяции в связанной кривой. Эти общие переменные выполняют не только интерполяцию на кривой, но и выполняют оценку неопределенности, интегрируя ее вклад в модель.

Важно понимать, что этот расчет не представляет собой то, что обычно делается, когда мы делаем это вручную, но оно объединяет все инструменты, доступные в моделировании модели, а также данные, полученные при моделировании связанной кривой.

REG_y (x). Интерполирует наблюдаемый отклик ( y ) указанного значения от оси x , оценивая связанную с ним общую неопределенность. Значение x может быть численным, переменным или даже частью модельного уравнения. Например, REG_y (5), REG_y (A) или REG_y (coef_a * ABS(A1-A2)).

REG_x (y). Учитывая значение, переменную или фрагмент уравнения, соответствующее оси y , интерполировать и оценить связанную неопределенность соответствующего значения x .

Неопределенность интерполяции.

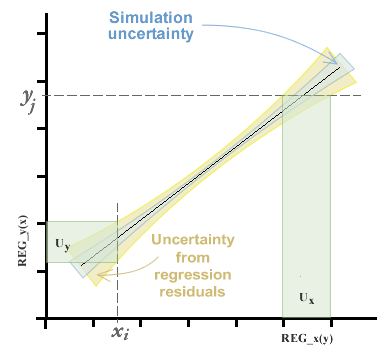
В главе Используя панель калибровочной кривой мы увидели, что мы можем оценить кривую наилучшего соответствия метод обыкновенных, обратных и полных наименьших квадратов (последний с помощью метода анализа первичной составляющей). Какой бы метод ни выбрали, мы получим коэффициенты уравнения линии в дополнение к диапазону переменной неопределенности вдоль кривой, состоящей из неопределенности моделирования и вклада в дисперсию остатков. Этот раздел можно увидеть более подробно в главе регрессий и кривых .

Тогда неопределенность в интерполяции будет дана стандартной ошибкой кривой на оси, из которой он намерен интерполировать.

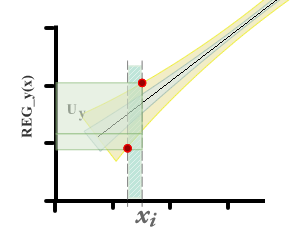
Можно видеть, что существуют два отличия в отношении метода, который обычно используется для оценки неопределенности в калибровочных кривых. Во-первых, нулевая неопределенность не ожидается на оси x .

С другой стороны, если вы хотите оценить значение x _i с помощью y _i , интервал неопределенности в x берется из остаточной дисперсии в x . На графиках вы можете увидеть представление неопределенности измеряемой величины в каждом случае.