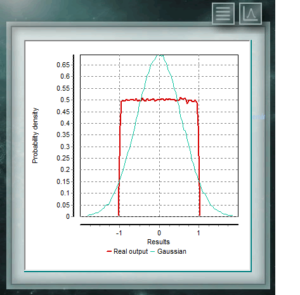
Это непрерывное распределение характеризуется одинаковой вероятностью для любого значения интервала. Он широко используется для вкладов неопределенностей типа B, в которых известны только основные и малые размеры интервала, например, в разделении или разрешении цифрового инструмента. Во многих случаях это распределение также может быть назначено, когда информации о случайной переменной мало, в библиографических данных или когда коэффициент покрытия неопределенности неизвестен,
Общая формула этого распределения определяется для всех значений x, для которых A ≤ x ≤ B, согласно уравнению:
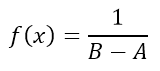
Входные параметры:
- Среднее. Среднее значение случайной величины.
- Полуинтервал. Соответствует середине интервала, к которому применяется это распределение, то есть (B-A) / 2, где A и B — верхняя и нижняя границы интервала. Если эта функция применяется к неопределенности с помощью разрешения цифрового инструмента, этот параметр будет соответствовать половине младшего деления (d / 2). Иногда это также относится к аналоговым инструментам, принимающим оценку (или оценку), как если бы это было оценочное деление, за пределами которого невозможно получить более визуальную информацию. В этом случае полуинтервал будет e / 2.
Дополнительная помощь
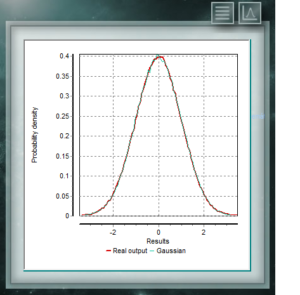Это распределение является тем, которое чаще всего представляет собой природные и социальные события. Значительная часть доказательств классической статистики, а также оценка неопределенностей основаны на предположении, что данные соответствуют нормальному распределению. С теоретической точки зрения Центральная предельная теорема утверждает, что, учитывая случайную выборку достаточно больших размеров, будет наблюдаться, что распределение сред следует приблизительно нормальному распределению. Общая формула этого распределения: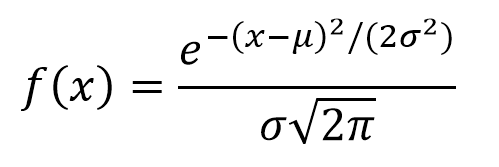
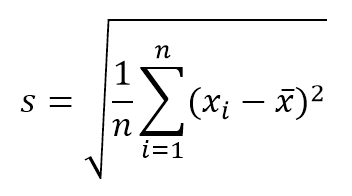
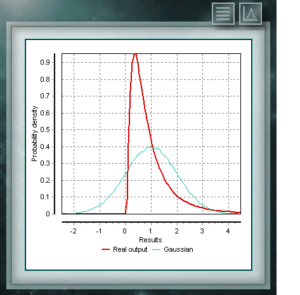Это распределение представляет случайные величины, логарифмы которых распределены в соответствии с нормальным распределением. Логнормальное распределение принимает различные формы в зависимости от значения его масштабного параметра и часто используется в надежности высокотехнологичных продуктов, а также в микробиологических подсчетах, поскольку они основаны на мультипликативной модели роста.
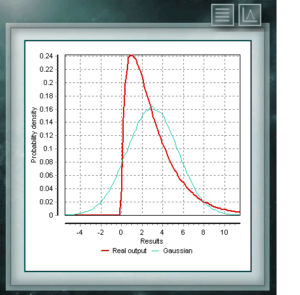Это непрерывное распределение вероятностей в поле положительных чисел тесно связано с нормальным распределением, например, это распределение образцов σ². Распределение Chi Ssquare определяется одним параметром, который является степенями свободы. Функция всегда асимметрична и смещена вправо. Это распределение очень часто используется в различных областях науки, поскольку оно позволяет анализировать наборы данных и определять, связано ли различие между ними случайностью (нулевая гипотеза) или другим внешним фактором.
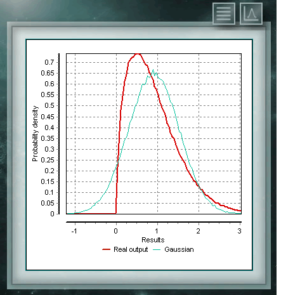Это распределение является непрерывной функцией в области положительных вещественных чисел, часто используемой в экономике, метеорологии и телекоммуникациях, а также в других конкретных приложениях, таких как уровень надежности или выживаемость организмов или машин. Случайные переменные, имеющие распределение распределения Вейбулла, распределяют ошибки в системах, когда коэффициент ошибки пропорционально связан с мощностью времени. Это распределение определяется из характеристического параметра формы (& gt; 0), который указывает на частоту отказа, так что, если скорость отказа уменьшается, она является постоянной или увеличивается со временем. Это соответствует, если параметр k меньше, равен или больше 1.
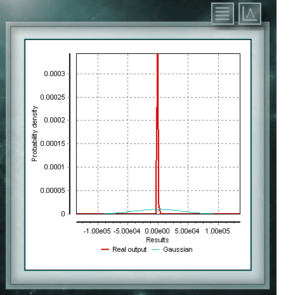Распределение Коши имеет особенность существования гауссовского типа распределений, однако оно имеет самый высокий пик, а хвосты разлагаются очень медленно. Хотя MCM Alchimia соответствующим образом генерирует псевдослучайные выборки для этого распределения, график результатов будет выглядеть как изолированный пик, поскольку ось абсцисс его берется в 99% -ном интервале вероятности покрытия. Поскольку распад хвостов настолько постепенный, диапазон значительных вероятностей становится очень узким.
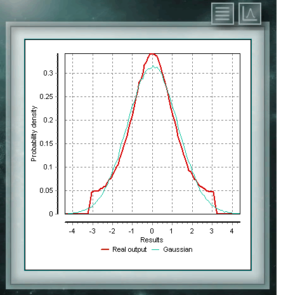Распределение фон Мизеса является непрерывной функцией круговых вызовов, т. Е. Они определены для реальных в интервале от 0 до 2π. В настоящее время эта функция используется предпочтительно в области эпидемиологии для описания распространения заболеваний или технологических применений, таких как обработка сигналов. Распространение фон Мизеса также известно как нормальный круговой , поскольку он подобен гауссову, но ограничен круговой плоскостью.
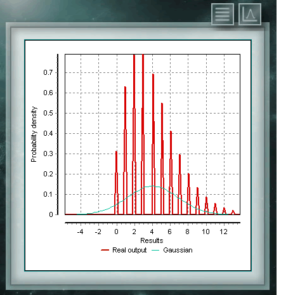Распределение Отрицательное биномиальное также является дискретным распределением, определенным в области положительных целых чисел. Он аналогичен биномиальному распределению, за исключением того, что параметр n относится к неточным и неполным событиям. Другими словами, случайная величина с Отрицательное биномиальное распределением параметров n и p представляет собой число успехов, вероятность которых равна p, которые достигаются в последовательности n неудачных испытаний. Параметры, с помощью которых определяется это распределение, имеют тот же вид, что и те, которые представляют биномиальное распределение, хотя, как мы сказали, параметр n представляет другое качество.
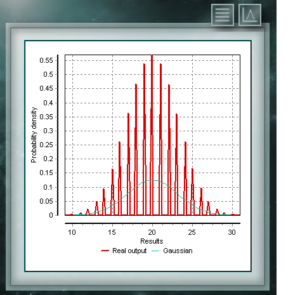Это дискретное распределение, домен которого является множеством положительных целых чисел, что представляет собой количество успехов, достигнутых в последовательности из n испытаний. Эти тесты должны иметь дихотомическую характеристику, т. Е. Предлагать в результате две возможности (успех и неудачу) и иметь определенную вероятность успеха = p.
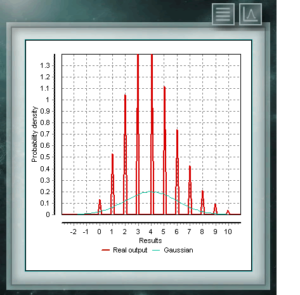Распределение Пуассона является дискретным распределением, определенным для области целых чисел, больших нуля. Он используется в основном для представления вероятности того, что определенное количество событий произойдет через определенный промежуток времени, определенное расстояние, площадь, объем и т. Д.