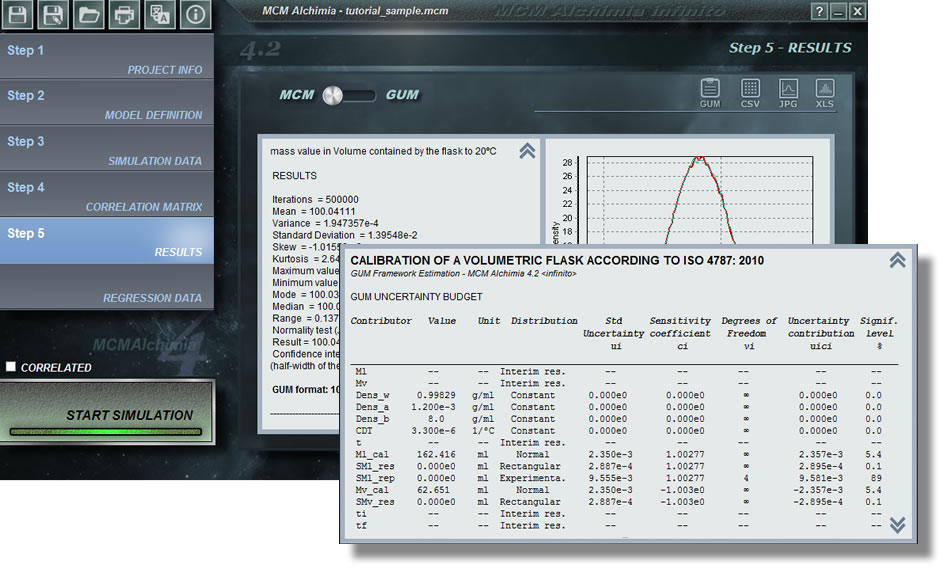
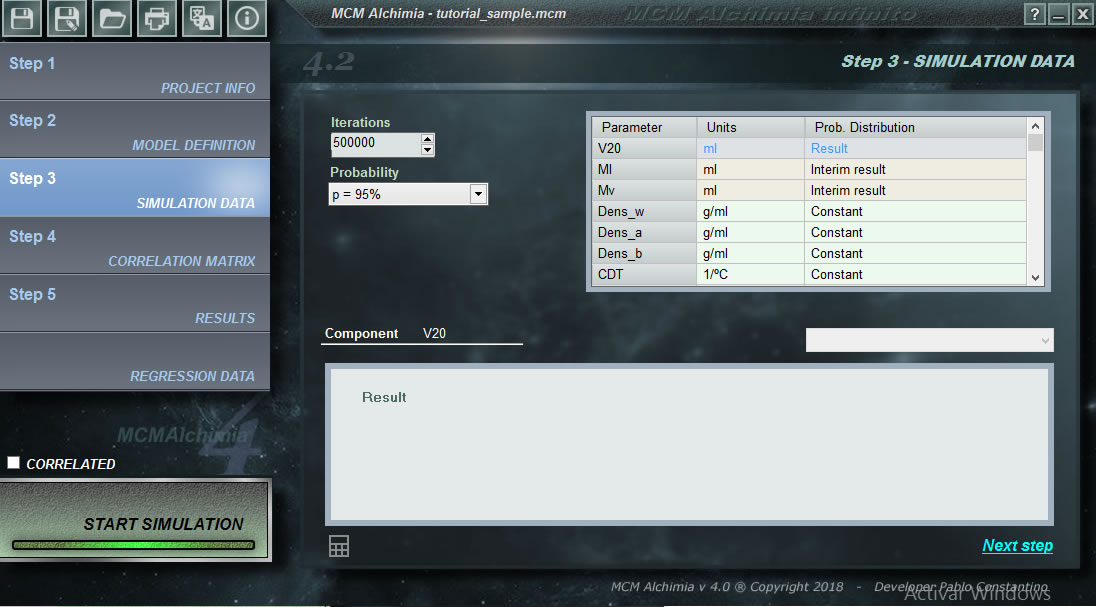
Хотя MCM Alchimia может использоваться в любой области, требующей моделирования методом Монте-Карло, инструмент был создан с учетом анализа неопределенности измерений. Вот почему многие из предопределенных опций уникальны в этом программном обеспечении и не будут найдены ни в одном подобном приложении (экспериментальное распределение, анализ калибровочных кривых или результат в классическом формате GUM в соответствии с JCGM 100). Ниже мы расскажем о некоторых советах и трюках, чтобы вы стали экспертом в использовании приложения и позволили получить более надежные и быстрые результаты в кратчайшие сроки.
1 .- Рекомендуемая последовательность действий
Хотя приложение очень интуитивно понятно, всегда полезно следовать последовательности работ, чтобы обеспечить как точность вычислений, так и эффективность использования времени. Методология работы можно обобщить на следующих этапах.
- Определение математической модели измеряемой величины. На этом этапе основная модель (уравнение) нашего исследования определяется так же, как мы обычно выполняем вычисления, или как это рекомендуется в наших справочных документах.
- Распределение входных величин в источниках неопределенности. Необходимо оценить все источники неопределенности, которые составляют каждую входную величину. Например, при использовании измерительного прибора будут иметься как минимум два источника неопределенности, один из которых должен быть калиброван, а другой — из-за разрешения (или разделения) оборудования. Но могут быть и налогоплательщики для дополнительных оценок (например, повторяемость). Мы рекомендуем диаграмму причинно-следственной связи, чтобы увидеть в целом налогоплательщиков модели.
- Напишите дополнительное уравнение в последующих строках для каждой величины базовой модели, которая имеет более одного источника неопределенности, используя префикс «S» для компонентов, которые будут принимать значение = 0 и будут включены только в неопределенность. Это лучше всего объясняется в следующем пункте.
- Убедитесь, что в каждом письменном уравнении число открываний круглых скобок равно количеству скобок закрытия.
- Перед назначением значений и распределений удобно сделать таблицу на бумаге со столбцами:
Переменная / Единицы / Значение (среднее) / Распределение вероятностей / Стандартное отклонение (или полуинтервация).
Это позволит увидеть все компоненты в общности модели. Эти данные затем будут напечатаны на шаге 3.
- Последующие шаги обеспечат успех в вашей оценке. Помните, что использование времени в вашем проекте будет составлять 80% для правильного проектирования математической модели (тестового уравнения).
2. Разделить большие модели на несколько простых уравнений
Мощный редактор уравнений MCM Alchimia infin позволяет вам писать неограниченное количество уравнений в текстовой области. Нет необходимости писать всю математическую модель эссе в одной строке. Чтобы избежать ошибок в скобках или других трудностей, которые трудно найти в конце, рекомендуется начать с базовой модели, содержащей общие переменные, а затем написать конкретные уравнения для каждой базовой величины. Вы можете увидеть пример решаемой модели, позже в справке, которая выполняется именно таким образом.
3. Правила редактора уравнений
Несмотря на то, что можно представить любую модель с MCM Alchimia, редактор уравнений имеет некоторые правила, которые хорошо помнить, чтобы избежать ошибок sintax.
- Все уравнения должны быть записаны в формате [measurand] = f ([variable 1] [variable 2] … [variable n]), то есть оба элемента уравнения должны быть включены.
- В модели может быть только одна величина вывода (измеряемая величина).
- Выходная величина должна быть в первой строке.
- Нельзя помещать «;» в конце строки возврат каретки (enter) в конце строки достаточно для разделения уравнений.
- Нельзя ставить два уравнения с одним и тем же промежуточным результатом.
- Редактор позволяет использовать символы ASCII (прописные буквы, строчные буквы, цифры и подсимволы и специальные символы виртуальной клавиатуры, которые могут отображаться с помощью кнопки αβ .) Например, имена переменных могут быть «Vol_p», «Temp2», «δ_724», «Δt» и т. Д. Не допускаются имена переменных, такие как «2_t» (по числу при запуске) или «ABS» (поскольку это ограниченный термин, это функция ).
- Переменные имена должны начинаться с буквенного символа и, кроме того, номера не могут использоваться в начале имени.
- Переменные имена чувствительны к регистру.
- Существуют зарезервированные термины, которые соответствуют функциям, которые не могут использоваться как имена переменных.
- Ссылка f(s) на область уравнений открывает клавиатуру функций, которые могут использоваться непосредственно в модели. Если часть уравнения отмечена, а затем с помощью клавиатуры выбрана функция, эта часть уравнения останется в качестве параметра функции.
- Также доступна ссылка с греческими буквами, которая позволяет включать символы из греческого алфавита в имена переменных.
4 .- Как включить переменные с различными источниками неопределенности
Очень распространенным случаем в тестах и калибровках является то, что величины имеют более одного источника неопределенности. Например, использование измерительного прибора может представлять несколько вкладов неопределенности из-за его калибровки, разрешения, повторяемости и т. Д. Чтобы включить все эти источники неопределенности, существует два способа:
- Величину можно разбить на столько же слагаемых, сколько источников неопределенности. Первый будет принимать измеренное или прочитанное значение (как среднее), а остальное будет распределением с нулевой точкой (среднее значение = 0), поскольку они будут использоваться только для оценки неопределенности и не будут влиять на результат. Например. температура, принятая в 10 раз, обеспечивая неопределенность для калибровки, разрешения и повторяемости, может быть выражена как:
T = T_cal + ST_res + ST_rep.
- Другой вариант заключается в том, чтобы разбить величину на константу, а затем на вкладчиков неопределенности, со средним значением = 0. Следуя предыдущему примеру:
T = T_value + ST_cal + ST_res + ST_rep
Обратите внимание, что переменные неопределенности, которые будут принимать нулевое значение, были записаны с использованием начального S. Хотя они могут принимать любое имя, хорошей практикой является разграничение имен с такими общими критериями. Таким образом, структура модели может быть известна уже из названия переменных.
5 .- Неопределенности типа A с MCM Alchimia
Очень распространенной ошибкой в использовании метода Монте-Карло для оценки неопределенностей является назначение функции распределения Обычный для величин, которые представляют неопределенности типа А, присваивая в качестве стандартного отклонения стандартное отклонение показаний.
Это даст ошибочные результаты неопределенности (под-оценки) из-за того, что учитывается небольшая информация о населении, то есть «степени свободы», используемые в подходе ГУМ. Полагая рассчитанное стандартное отклонение напрямую, предполагается, что эта величина имеет бесконечные степени свободы, что неверно.
Существует три способа включения правильно типа неопределенности в MCM Alchimia
- JCGM 101 Оценка руководства по измерению данных — Приложение 1 к. «Руководство по выражению неопределенности в измерении» указывает, что для неопределенностей типа А следует использовать распределение Стьюдента (масштабирование и сдвиг) вместо гауссовского. Для этого распределения в качестве параметра указывается степень свободы, так что уровень информации, который у вас есть, будет включен.
- Если вы хотите использовать нормальное распределение, это также можно сделать, хотя в качестве стандартного отклонения необходимо ввести отклонение, рассчитанное в нашем тесте, умноженное на коэффициент покрытия для наших степеней свободы и 95,45% вероятности покрытия (Student t), разделенное 2. Эта простая операция позволит моделировать с учетом степеней свободы величины.
- Наша рекомендация. Эксклюзивная спецификация MCM Alchimia — это включение FDP под названием Experimental. Эта мощная панель позволяет нам работать с неопределенностями типа А непосредственно из исходных значений нашего теста, без необходимости вычислять стандартное отклонение или другую операцию с нашей стороны. Используя эту опцию, приложение автоматически рассмотрит проблему степеней свободы, стандартных отклонений и т. Д. Их можно даже использовать для более сложных моделей повторяемости, для образца / стандарта / образца и других.
Дополнительная помощь
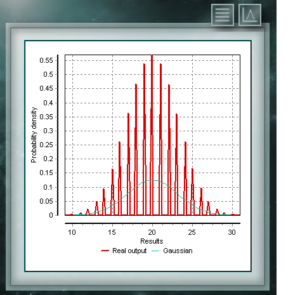Это дискретное распределение, домен которого является множеством положительных целых чисел, что представляет собой количество успехов, достигнутых в последовательности из n испытаний. Эти тесты должны иметь дихотомическую характеристику, т. Е. Предлагать в результате две возможности (успех и неудачу) и иметь определенную вероятность успеха = p.
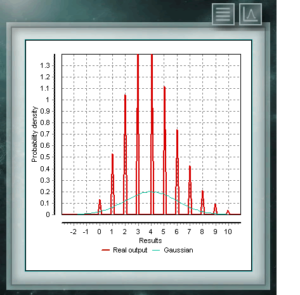Распределение Пуассона является дискретным распределением, определенным для области целых чисел, больших нуля. Он используется в основном для представления вероятности того, что определенное количество событий произойдет через определенный промежуток времени, определенное расстояние, площадь, объем и т. Д.
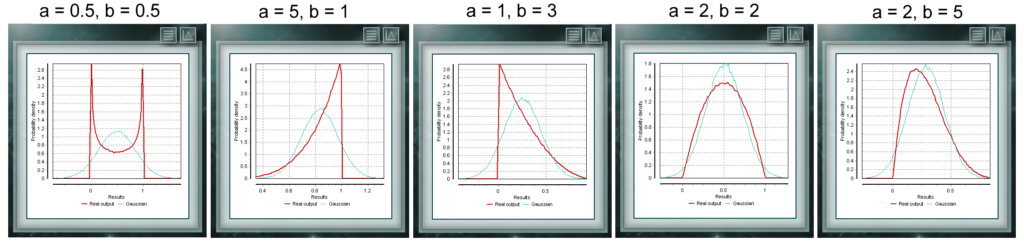Это распределение является непрерывной функцией с двумя параметрами, которые должны принимать реальные значения, большие нуля. Функция определяется между 0 и 1. Частный случай бета-распределения — это когда оба параметра формы принимают значения = 1. В этом случае функция будет совпадать с равномерным распределением.
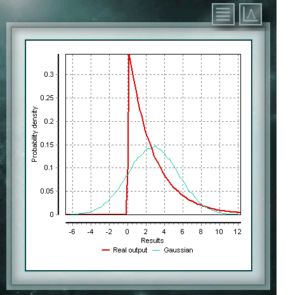Экспоненциальное распределение вероятностей является непрерывной функцией в области положительных чисел, что подходит для представления времени между двумя событиями, распределенными в соответствии с распределением пуассонов. Например, до тех пор, пока торговля не получит своего первого клиента в тот день. Экспоненциальное распределение является частным случаем распределения Гамма, где параметр формы принимает значение 1.
Это распределение является непрерывной функцией смещенного характера, то есть, когда модальное значение не соответствует среднему значению. Распределение Гамма является обобщением экспоненциального распределения и используется в общем случае для моделирования случайных величин, которые представляют время, в течение которого событие происходит определенное количество раз.
