Данные моделирования
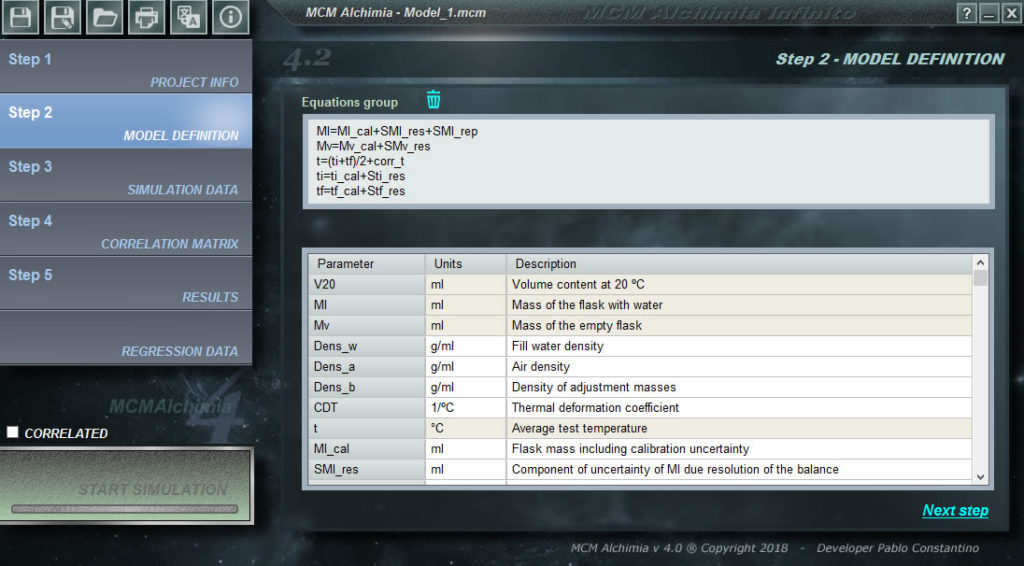
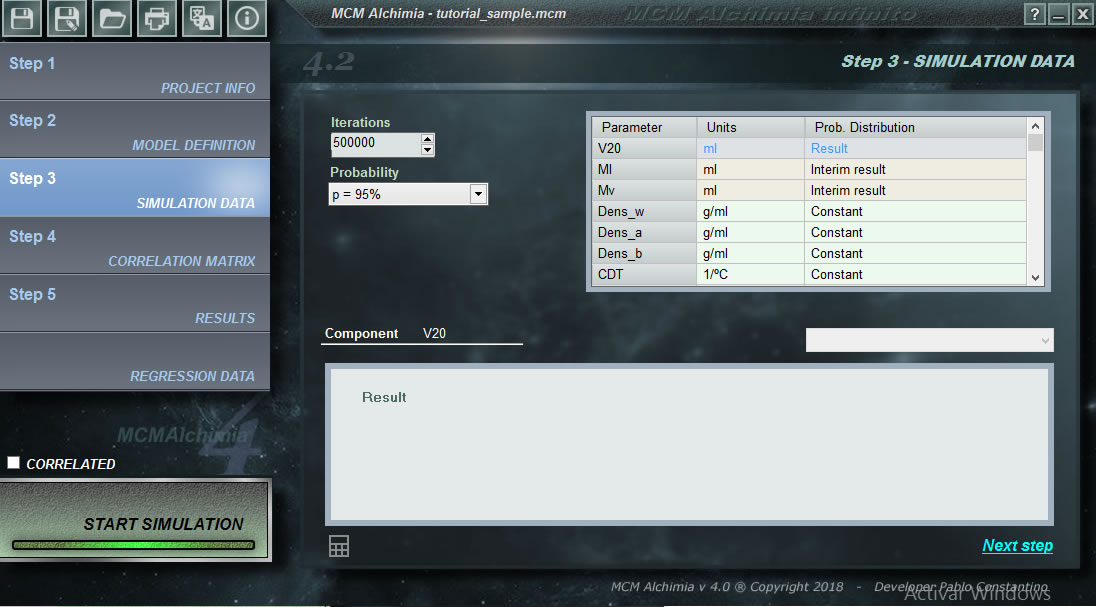
Единственное, что нам осталось сделать в нашем первом проекте, — это присвоить функцию распределения вероятности каждой случайной переменной, которая представляет наш проект. Как видно из программы, сетка состоит из нескольких строк, некоторые из них с белым фоном, а другие с серым фоном. Строки с серым фоном соответствуют величинам, для которых функция распределения не может быть назначена, поскольку они представляют собой промежуточные результаты или конечный результат, то есть величины, которые будут получены при моделировании в результате вторичных уравнений.
В нижней части рабочей панели есть окно команд, которое даст нам раскрывающийся список функций распределения вероятности, чтобы мы могли выбрать тот, который соответствует входной величине. После того, как мы выбрали распределение вероятности, в нижнем поле мы попросим ввести необходимые параметры для моделирования. Поэтому процесс этого шага будет следующим:
- Рекомендуется оставить число итераций в 500000, так как оно получено в превосходной производительности в приложении, и результаты абсолютно надежны с этим количеством итераций (можно ознакомиться с документом: Вычислительные аспекты при оценке неопределенностей теста методом Монте-Карло (только на испанском языке)
- Мы выбираем вероятность покрытия результатов. Для получения результатов для K = 2 рекомендуется использовать 95,45%.
- Мы нажимаем на первую строку с белым фоном (или мы достигаем ее клавишами курсора нашей клавиатуры)
- Мы выбираем функцию распределения вероятности в раскрывающемся списке.
- Мы заполняем параметры моделирования на нижней панели (пожалуйста, учитывайте единицы измерения).
- Мы нажимаем «Применить». Если все правильно, строка будет иметь зеленый фон, что указывает на правильность присвоения им данных моделирования.
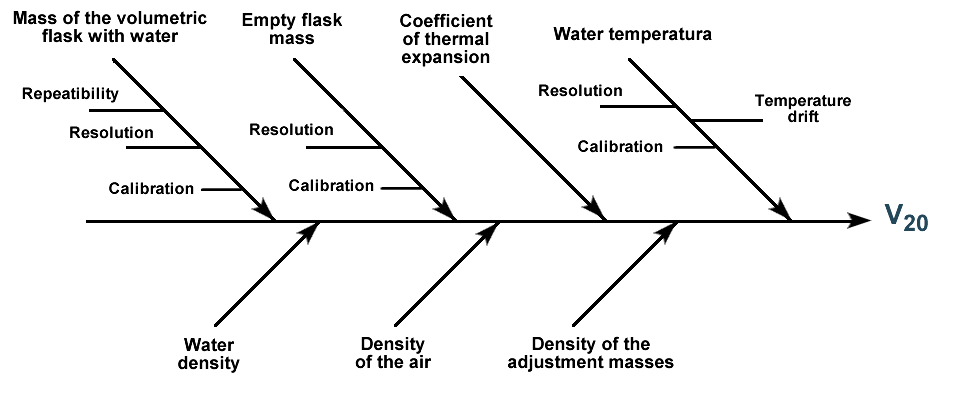
Возвращаясь к нашей мерной колбе, мы получим так:
- V20 : отключено, потому что оно Результат, невозможно присвоить функцию распределения вероятности
- Ml : отключено, поскольку оно Промежуточный результат . Невозможно назначить распределение вероятности.
- Mv : отключено, потому что оно Промежуточный результат . Невозможно назначить распределение вероятности.
- Dens_w : мы назначим элемент Константа со значением = 0.99829 (г / мл)
- Dens_a : присвойте элементу константу значение Value = 1.2E-3 (g / ml)
- Dens_b : мы назначим элемент Константа со значением = 8000 (г / мл)
- CDT . Назначьте элемент Константа со значением = 3.3E-6 (1 / ºC)
- t : отключено, потому что оно Промежуточный результат . Невозможно назначить распределение вероятности
- Ml_cal . Из-за расширенной неопределенности мы назначим распределение Нормальный со средним значением наших показаний, Среднее значение = 162 416, вводя информацию сертификата в «Использовать сертификат «, с неопределенностью = 0,0047 (g) и k = 2
- SM_res . Мы назначим дистрибутив Rectangular со значением Mean = 0 (соответствующий всем переменным, которые вводятся только с целью оценки неопределенностей) и Half interval = 0,0005, то есть половину деления цифровой шкалы взвешивания.
- SM_rep . Для повторяемости MCM Alchimia предоставляет экспериментальное распределение, в котором мы можем непосредственно помещать измеренные значения, и приложение будет отвечать за внесение необходимых нам статистических расчетов, использовать для моделирования , Поскольку для целей неопределенности мы должны выбрать «Среднее = 0». Мы будем использовать опцию «Прямой» и нажав кнопку «Значения», мы введем 5 показаний нашего эссе: 162 384; 162431; 162409; 162,417; 162,439
- Mv_cal . Из-за расширенной неопределенности мы назначим распределение Нормальное со средним значением при чтении баланса, чтобы взвесить пустую колбу, Среднее = 62.651, ввод информации сертификата в «Использовать сертификат», с неопределенностью = 0.0047 (g) и k = 2
- SMv_res . Мы назначим дистрибутив Прямоугольный , с Media = 0 и Half interval = 0.0005.
- ti : отключено, потому что оно Промежуточный результат . Невозможно назначить дистрибутив
- tf : отключено, потому что оно Промежуточный результат . Невозможно назначить распределение вероятности.
- corr_t : мы назначим элемент Константа со значением = -0.022 (ºC)
- ti_cal . Поскольку он получен из сертификата калибровки, мы присваиваем PDF Normal значение нашего считывания среднего термометра = 20.05. В то же время мы выберем «Использовать сертификат», и мы добавим расширенную неопределенность = 0,021 (ºC) и k = 2.
- Sti_res . Для этой меры мы используем ртутный термометр в стекле деления: 0,1ºC, из которого мы можем визуально оценить 1/4 деления. В соответствии с этим мы назначим распределение Треугольное со средним = 0 и полуинтервалом = 0,125 (это оценка / 2)
- tf_cal : то же самое, что и в ti_cal, но теперь нашим средним будет конечная температура: Среднее = 20 075, выберите «Использовать сертификат» и укажите расширенную неопределенность = 0,021 (ºC) и k = 2.
- Stf_res : То же, что и Sti_res, т. е. Треугольное с Media = 0 и полуинтервал = 0.125.
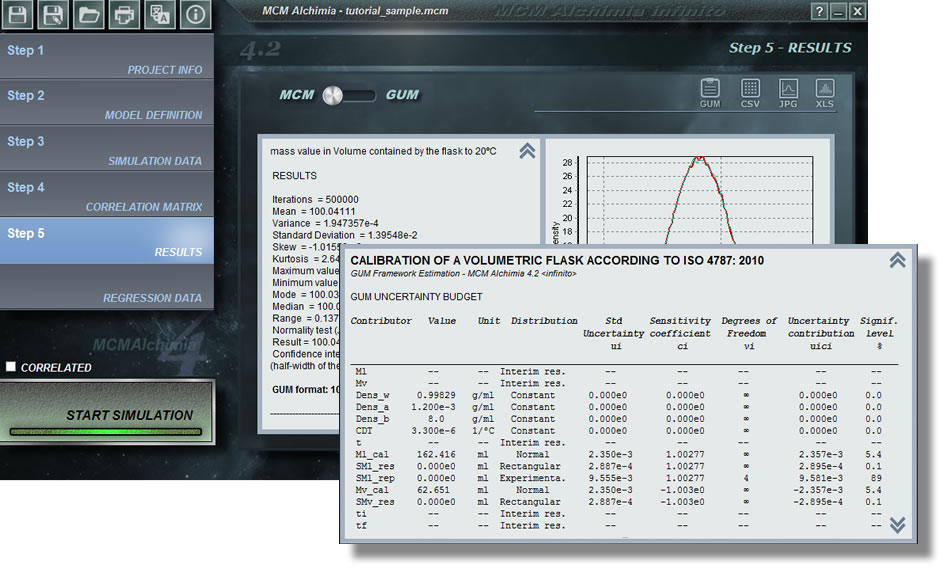
При вводе данных для последней величины загорается кнопка «Запустить симуляцию», чтобы мы могли запустить нашу симуляцию и получить результаты. Смотреть результаты после моделирования .
Дополнительная помощь