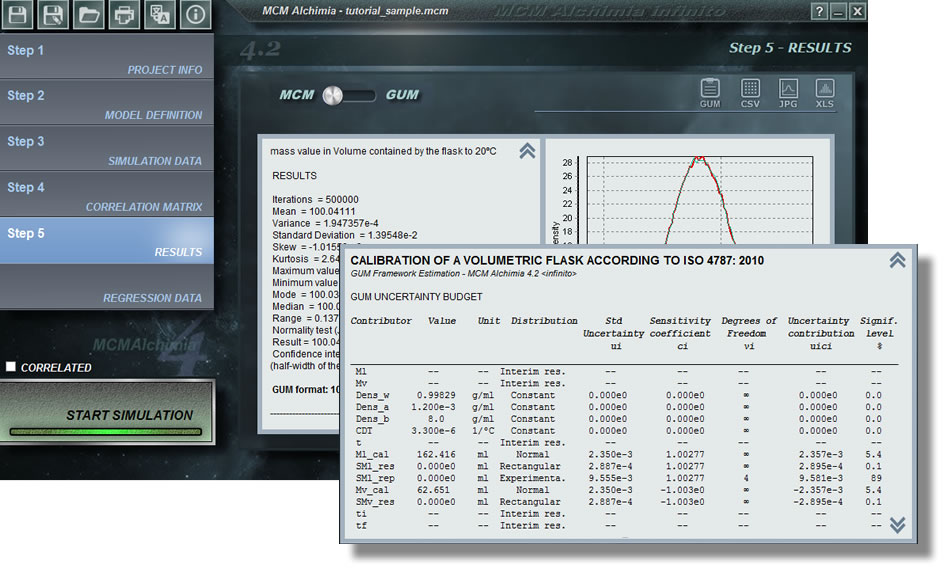
While MCM Alchimia can be used in any scope that requires Monte Carlo simulations, the tool has been created with the measurement uncertainty analysis in mind. This is why many of the predesigned options are unique in this software and will not be found in any similar applications (experimental distribution, analysis of calibration curves, or the result in classic GUM format according with JCGM 100). Below we detail some tips and tricks for you to become an expert in the use of the application and allow more reliable and faster results in no time.
1 .- Recommended workflow
While the application is very intuitive it is always good to follow a sequence of work to ensure both the accuracy of the calculations as well as the efficiency in the use of time. The work’s methodology can be summarized in the following stages.
- Definition of the mathematical model of the measurand. In this stage, the basic model (equation) of our trial is defined, just as we usually perform the calculations, or like is recommended in our reference documents.
- The breakdown of input quantities into sources of uncertainty. It is necessary to evaluate all the sources of uncertainty that make up each input quantity. For example, when using a measuring instrument at least two sources of uncertainty will be had, one due to calibration and another due to the resolution (or division) of the equipment. But there may also be taxpayers for additional evaluations (for instance repeatability). We recommend a Cause-Effect diagram to see in general the taxpayers of the model.
- Write an additional equation in subsequent rows for each magnitude of the basic model that has more than one source of uncertainty using the prefix “S” for the components that will take value = 0 and will only be included by uncertainty. This is best explained in the next item.
- Verify that, in each written equation, the number of parentheses opening is equal to the number of parentheses closing.
- It is convenient before assigning the values and distributions to make a table on paper with the columns:
Variable / Units / Value (Mean) / Probability distribution / Standar deviation (or semi-interval).
This will allow to see each components in the generality of the model. These data will then be typed in Step 3.
- Following these steps will ensure success in your estimation. Remember that the use of time in your project will be 80% dedicated to the correct design of the mathematical model (the test equation).
2 .- Divide large models into several simple equations
The powerful equation editor of MCM Alchimia infinite allows you to write an unlimited number of equations in the text area. It is not necessary to write the entire mathematical model of the essay in a single line. To avoid making errors of parenthesis balance or others difficult to find at the end, it is advisable to start with a basic model that contains general variables and then write specific equations for each base quantity. You can see the example of a solved model, later in the help, which is done just in this way.
3 .- Equation editor rules
Even though is possible to represent any model with MCM Alchimia, the equation editor has some rules that it is good to remember to avoid sintax errors.
- All equations must be written in the format [measurand] = f([variable 1],[variable 2],…,[variable n]), that is, both members of the equation must be included.
- There can only be one magnitude of output in the model (measurand)
- The output magnitude must be on the first line
- It is not allowed to put “;” at the end of the line, the carriage return (enter) at the end of the line is enough to separate equations
- It is not allowed to put two equations with the same intermediate result.
- The editor allows ASCII characters (uppercase letters, lowercase letters, numbers and sub-characters and special characters of the virtual keyboard that can be displayed with the αβ button. Example of variable names can be “Vol_p”, “Temp2”, “δ_724”, “Δt”, etc. It is not allowed variable names like “2_t” (by number at start) or “ABS” (since it is a restricted term, it is a function)
- Variable names must be started with an alphabetic character and moreover, numbers can not be used at the beginning of the name.
- Variable names are case-sensitive.
- There are reserved terms that correspond to functions, which can not be used as variable names.
- The f(s) link on the area of equations opens a keypad of functions that can be used directly in the model. If a portion of the equation is marked and then a function is selected with the keypad, this portion of the equation will remain as a parameter of the function.
4 .- How to include variables with various uncertainty contributors
A very common case in tests and calibrations is that the magnitudes have more than one source of uncertainty. For instance, the use of a measurement instrument may present several uncertainty contributions due to its calibration, resolution, repeatability, etc. To include all these sources of uncertainty, there are two ways to proceed:
- The magnitude can be broken down into as many addends as sources of uncertainty. The first one will take the measured or read value (as average) and the rest will be zero-centered distributions (average value = 0) since they will only be used to evaluate the uncertainty and will not influence the result. E.g. a temperature taken 10 times providing uncertainties for calibration, resolution and repeatability can be expressed as:
T = T_cal + ST_res + ST_rep.
- The other option is to break down the magnitude into a constant and then the uncertainty contributors, all with average value = 0. Following the previous example would be:
T = T_value + ST_cal + ST_res + ST_rep
Note that the variables for uncertainty, which will take zero value, were written with an initial S. While they can take any name, it is good practice to differentiate names with a common criteria like this. In this way, the structure of the model can be known already from the name of the variables.
5 .- Type A uncertainties with MCM Alchimia
A very common error in the use of the Monte Carlo method for the estimation of uncertainties is the assignment of the Normal Distribution Function to the magnitudes that present “type A” uncertainties, assigning, as standard deviation, the standard deviation of the readings.
This will yield erroneous uncertainty results (sub-estimates) due to the fact that little information about the population is taken into account, that is, the “degrees of freedom” as used in the GUM approach. By putting the calculated standard deviation directly, it is assuming that this magnitude has infinite degrees of freedom, which is not correct.
There are three ways to include correctly type A uncertainties in MCM Alchimia
- The JCGM 101 Evaluation of measurement data guide – Supplement 1 to the. “Guide to the expression of uncertainty in measurement” , indicates that for type A uncertainties a Student t distribution (scaled and shift) should be used, instead of a Gaussian one. For this distribution it should be indicated, as a parameter, the degrees of freedom, so that the level of information that you have of the magnitude will be included.
- In case you want to use the normal distribution, it can also be done, although as a standard deviation the deviation calculated in our test should be entered, multiplied by the coverage factor for our degrees of freedom and 95.45% coverage probability (inverse t distribution), divided 2. This simple operation will allow simulation taking into account the degrees of freedom of the magnitude.
- Our recommendation. An Exclusive specification of MCM Infinite Alchimia, is the inclusion of an FDP called Experimental. This powerful panel allows us to work with type A uncertainties directly from the raw values of our test, without the need to calculate any standard deviation or other operation on our part. Using this option, the application will automatically deal with the problem of degrees of freedom, standard deviations, etc. They can even be used for more complex repeatability models, for Sample / Standard / Sample and others.
More help
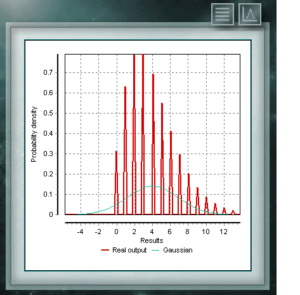 The NegBinomial distribution is discrete distribution, defined in the domain of positive integers. It is similar to the binomial distribution except that the n parameter refers to non-total and incomplete events. In other words, a random variable with NegBinomial distribution of parameters n and p represents the number of successes whose probability is p, which are achieved in a sequence of n failed trials. The parameters by means of which this distribution is defined have the same form as those that represent the Binomial distribution, although, as we said, the parameter n represents a different quality.
The NegBinomial distribution is discrete distribution, defined in the domain of positive integers. It is similar to the binomial distribution except that the n parameter refers to non-total and incomplete events. In other words, a random variable with NegBinomial distribution of parameters n and p represents the number of successes whose probability is p, which are achieved in a sequence of n failed trials. The parameters by means of which this distribution is defined have the same form as those that represent the Binomial distribution, although, as we said, the parameter n represents a different quality.

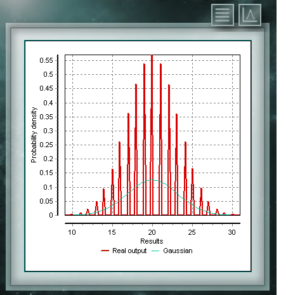 Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.
Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.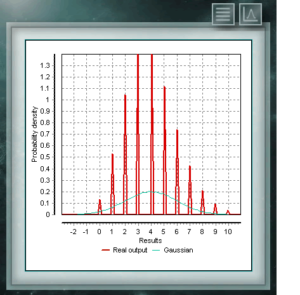 The Poisson distribution is a discrete distribution defined for the domain of integers greater than zero. It is used mostly to represent the probability that a certain number of events will occur in a period of time, a defined distance, area, volume, etc.,
The Poisson distribution is a discrete distribution defined for the domain of integers greater than zero. It is used mostly to represent the probability that a certain number of events will occur in a period of time, a defined distance, area, volume, etc.,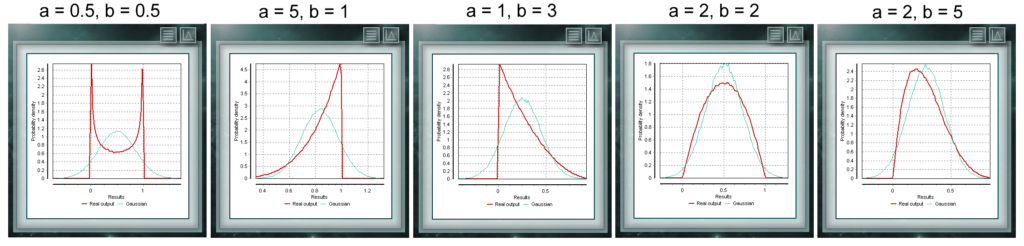 This distribution is a continuous function with two parameters which must take real values greater than zero. The function is defined between 0 and 1. A particular case of the Beta distribution is when both form parameters take values = 1. In this case the function will coincide with a uniform distribution.
This distribution is a continuous function with two parameters which must take real values greater than zero. The function is defined between 0 and 1. A particular case of the Beta distribution is when both form parameters take values = 1. In this case the function will coincide with a uniform distribution. The exponential probability distribution is a continuous function in the domain of positive reals, which is suitable to represent the time between two events that are distributed according to the Poisson distribution. For example, the elapse until a trade receives its first customer of th day. The exponential distribution is a particular case of the Gamma distribution where shape parameter takes value 1.
The exponential probability distribution is a continuous function in the domain of positive reals, which is suitable to represent the time between two events that are distributed according to the Poisson distribution. For example, the elapse until a trade receives its first customer of th day. The exponential distribution is a particular case of the Gamma distribution where shape parameter takes value 1.