Regression
NOTE: This tool is only available for models with connected curves (See work with curves)
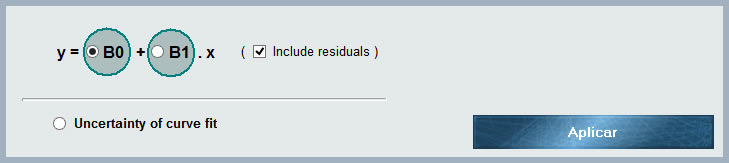
At the end of the list of distributions, MCM Alchimia have available this tool that allows to assign regression parameters to our test model. In this way, we have 3 options related to our connected curve to choose from:
- B0. Independent coefficient (ordinate at the origin) of the connected curve.
- B1. Coefficient of the first order of the connected curve.
Both B0 and B1 will have associated uncertainties that correspond to the result of the simulation, that is, if at least one of the values used to construct the curve had uncertainty, the simulation will necessarily produce a succession of curves for each set of simulated values, each with coefficients B0 and B1 that will have some degree of variation. The magnitude of this variation is related to the magnitude of the uncertainty of the input data in both axes.
- Include residuals. If this option is selected, the uncertainties associated with the coefficient we have selected (B0 or B1) will be used increased by a quantity determined by the contribution due to least squares residuals . Thus, the uncertainty associated with both parameters will include simulation and waste contributions
- Uncertainty due to adjustment. If we assign this option to our parameter, what we will obtain is the standard uncertainty of the connected curve due to residuals, centered at zero (only as contribution of uncertainty). This value is found in regressions made in spreadsheet such as typical error or standard error of regression.
Note : It is important to note that if we simulate the typical error of a curve in isolation, the standard deviation result of the resulting population is a little larger than the same parameter obtained in a spreadsheet. This is because although the variable is defined as mean 0 and deviation = to the standard uncertainty, the simulation distribution in MCM Alchimia for this case is not a Normal, but a Student t with the degrees of freedom that determine the Number of points with which the curve was built, resulting in a greater deviation for the measurand.

