Triangular distribution
 The continuous triangular distribution is characterized by being bounded to two extremes as in the case of the rectangular, but also has a mode (or value more probabe) within that range. The probability in any subinterval of equal length will increase linearly until fashion and then descend in the same way to the upper bound. This distribution is widely used in variables where information is limited, as in the case of the uniform, but where we have an approximate knowledge of the Modal value, that is, where, although the exact point of this value is not known, has information of the region or subinterval where to find it.
The continuous triangular distribution is characterized by being bounded to two extremes as in the case of the rectangular, but also has a mode (or value more probabe) within that range. The probability in any subinterval of equal length will increase linearly until fashion and then descend in the same way to the upper bound. This distribution is widely used in variables where information is limited, as in the case of the uniform, but where we have an approximate knowledge of the Modal value, that is, where, although the exact point of this value is not known, has information of the region or subinterval where to find it.
Important: In the case of MCM Alchimmia, only the centered triangular is available, that is, the statistical mode corresponds to the average value of the AB interval.
The general equation will then be defined for the interval AB, while outside those extremes the distribution function will be 0. The formula will then be:
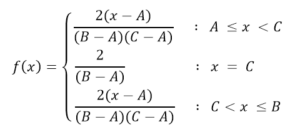
Input parameters:
- Average. Mean value and modal value of the random variable.
- Semi-interval. Corresponds to the middle of the interval to which this distribution is applied, that is (B-A) / 2, where A and B are the upper and lower bounds of the interval. When this function is applied to the uncertainty by resolution of an analog instrument, this parameter will correspond to the appreciation (or estimate & lt; e & gt;). Also in the area of chemistry it is usual to take the tolerance of the volumetric material or even the reference materials as contributors of uncertainty of tringular distribution (EURACHEM/QUAM:2012 8.1.6). In both mentioned cases, the semi-interval will correspond to the value and tolerance of the material.
More help

