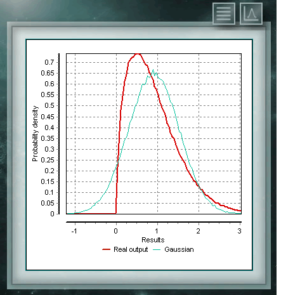
This distribution is a continuous function in the domain of positive real numbers, frequently used in economics, meteorology and telecommunications, as well as other specific applications, such as the reliability rate or the survival of organisms or machines. The random variables that have the Weibull distribution model the distribution of faults in systems when the fault ratio is proportionally related to a power of time. This distribution is defined from a characteristic Form (> 0) parameter that would indicate the failure rate, so that if the failure rate decreases, it is constant or increases with time. That corresponds with if the parameter k is smaller, equal or greater than 1.
Input parameters:
- Shape. This parameter defines the shape of the distribution. You can take as a value any field number of reals greater than zero.
- Scale. This second parameter allows to scale the resulting values generating pseudo-random with the same form but greater standar deviation.
More help
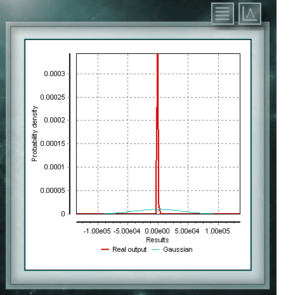The Cauchy distribution has the particularity of being of the Gaussian type of distributions, however it has the highest peak and the tails decompose very slowly. Although MCM Alchimia suitably generates the pseudo-random samples for this distribution, the results graph will look like an isolated peak since the abscissa axis of it is taken in the 99% coverage probability interval. Because the decay of the tails is so gradual, the range of significant probabilities becomes very narrow.
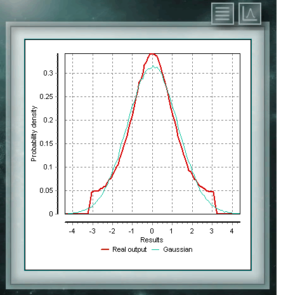The distribution of Von Mises is a continuous function of the circular calls, that is, they are defined for the real ones in the interval from 0 to 2p. This function is currently used preferably in the field of epidemiology to describe the spread of diseases or technological applications such as signal processing. The Von Mises distribution is also known as normal circular as it is similar to Gaussian, but restricted to the circular plane.
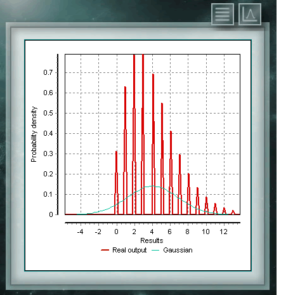The NegBinomial distribution is discrete distribution, defined in the domain of positive integers. It is similar to the binomial distribution except that the n parameter refers to non-total and incomplete events. In other words, a random variable with NegBinomial distribution of parameters n and p represents the number of successes whose probability is p, which are achieved in a sequence of n failed trials. The parameters by means of which this distribution is defined have the same form as those that represent the Binomial distribution, although, as we said, the parameter n represents a different quality.
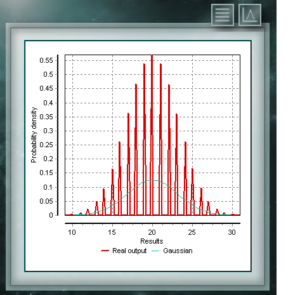Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.
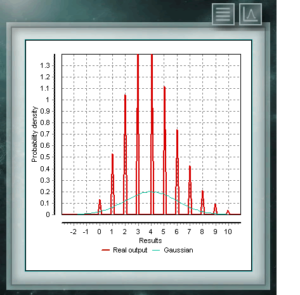The Poisson distribution is a discrete distribution defined for the domain of integers greater than zero. It is used mostly to represent the probability that a certain number of events will occur in a period of time, a defined distance, area, volume, etc.,
This distribution is a continuous function with two parameters which must take real values greater than zero. The function is defined between 0 and 1. A particular case of the Beta distribution is when both form parameters take values = 1. In this case the function will coincide with a uniform distribution.
The exponential probability distribution is a continuous function in the domain of positive reals, which is suitable to represent the time between two events that are distributed according to the Poisson distribution. For example, the elapse until a trade receives its first customer of th day. The exponential distribution is a particular case of the Gamma distribution where shape parameter takes value 1.