29 November, 2017 – MCM Alchimia

NOTE: This tool is only available for models with connected curves (See work with curves)

At the end of the list of distributions, MCM Alchimia have available this tool that allows to assign regression parameters to our test model. In this way, we have 3 options related to our connected curve to choose from:

B0. Independent coefficient (ordinate at the origin) of the connected curve.
B1. Coefficient of the first order of the connected curve.

Both B0 and B1 will have associated uncertainties that correspond to the result of the simulation, that is, if at least one of the values used to construct the curve had uncertainty, the simulation will necessarily produce a succession of curves for each set of simulated values, each with coefficients B0 and B1 that will have some degree of variation. The magnitude of this variation is related to the magnitude of the uncertainty of the input data in both axes.

Include residuals. If this option is selected, the uncertainties associated with the coefficient we have selected (B0 or B1) will be used increased by a quantity determined by the contribution due to least squares residuals . Thus, the uncertainty associated with both parameters will include simulation and waste contributions
Uncertainty due to adjustment. If we assign this option to our parameter, what we will obtain is the standard uncertainty of the connected curve due to residuals, centered at zero (only as contribution of uncertainty). This value is found in regressions made in spreadsheet such as typical error or standard error of regression.

Note : It is important to note that if we simulate the typical error of a curve in isolation, the standard deviation result of the resulting population is a little larger than the same parameter obtained in a spreadsheet. This is because although the variable is defined as mean 0 and deviation = to the standard uncertainty, the simulation distribution in MCM Alchimia for this case is not a Normal, but a Student t with the degrees of freedom that determine the Number of points with which the curve was built, resulting in a greater deviation for the measurand.

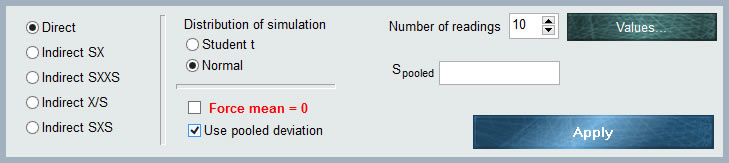
This distribution is not a distribution in itself, but a powerful and exclusive form of MCM Alchimia to enter raw values of repeatability to the model of our trial without having to make any kind of previous operations in a spreadsheet.

As can be seen in the graph, the entry data panel has several selectors to define the input characteristics of our uncertainty component.

1. Input data set

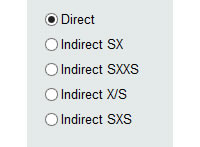To the left of the panel we have 5 radio buttons (selectors), which will indicate to the software the form in which the input data will be entered. We will then have 5 input forms:

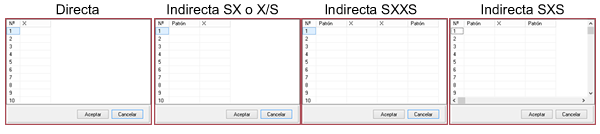
Direct. By selecting this option we will be telling MCM Alchimia that we will enter the data one by one. From these data, the software will automatically obtain the mean, standard deviation of the sample means and degrees of freedom, statistics parameters necessary to perform the simulation.
Indirect SX. This option indicates that we want the application to request two columns of data, of which each value for repeatability will be obtained from the subtraction Value = (X – S ) . An example where this option can be used is when two digital instruments are calibrated by comparison, and you want to calculate the repeatability of the errors. We indicate the reading of the pattern in the column of S and the reading of the sample in X. It can also be used when it is desired to obtain the weight of a substance contained in a crucible, through the weight of the empty crucible and with the content. In this case, the mass values of the empty crucible can be indicated in S and the mass of the crucible with the contents in X.
Indirect SXXS. In certain cases the error values are obtained from a set of measures also known as ABBA format, which will be requested in a table of 4 columns. This format is sometimes used when it is desired to eliminate the bias caused by the potential drift of the measuring instruments. In this way, each value will be obtained from the calculation Value = (X1 + X2) / 2 – (S1 + S2) / 2 .
Indirect X / S. In this indirect format, each value for repeats will be obtained from the Value = X / S relationship, indicated through a table of two columns.
Indirect SXS. This format is similar to SXXS, only in three columns. The values will be obtained automatically by the application, through the operation: Value = X – (S1 + S2) / 2 .

2. Income of values.

In the upper right corner of the MCM panel Alchimia has a field where we must indicate the number of repetitions to which we want to estimate the simulation parameters, that is, the mean and the standard deviation of the stockings By default the application has 10 values, however this value can be changed by manually editing the number or with the increment / decrement arrows.

After indicating the number of measurements that will be entered, we click on the “Values” button, where a grid will open for the entry of values. According to the income format chosen in the radio buttons selector, the table will have the number of columns required:

3.- Simulation distribution.

This section of the panel provides two ways to perform the simulation from the parameters of the previously defined distribution from the entered values:

Student t distribution. Selecting this option, MCM Alchimia will calculate the mean and standard deviation of the sample means from the table of values entered. Then it will generate randomized distributed according to the Student t function, with a number of degrees of freedom equal to the number of values -1.

Normal. In this case, the software will perform the same calculations as before, then take the inverse value of the function t (coverage factor k ) for the chosen coverage probability and the degrees of freedom calculated. The simulation will then be done with pseudo-randomized normal distribution of calculated mean and standard deviation s1 = ks / k ‘ , being k’ the inverse value of the distribution t for the same probability of coverage, but infinite degrees of freedom.

For a high number of degrees of freedom, both simulations will have similar or identical characteristics. In contrast, for a number of degrees of freedom <10 The results obtained from both simulations could present significant differences. Then which one to choose?

Depending on the utility that we want to give to this application, we may require one or another simulation distribution, but for technicians who are not experts in statistics, we recommend following the following rule:

For validation of traditional calculation estimates according to GUM (JCGM 101), routine laboratory tests, proficiency tests, GUM vs MCM validation, etc. simulate according to a Normal distribution.
For research, statistics, economics and cases where it is necessary to know accurately the impact of a variable on the uncertainty of the measurand, simulate according to a Student t distribution.

4. Forcing Mean = 0.

This option is foreseen when we want the taxpayer to whom this distribution applies only to be entered for uncertainty purposes. In this way, the average value of the function will be canceled so that the mean is = 0 and does not provide value. This is especially useful when we have model components that have more than one uncertainty, for example resolution and repeatability. In this way it can be indicated as summed variables, one constant with the value of the parameter and the rest only as contributors of uncertainty with zero value. In this case Type A can be put as experimental. The example of this help uses this tool.

Regression

Experimental (raw data)