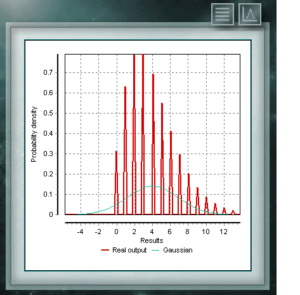
The NegBinomial distribution is discrete distribution, defined in the domain of positive integers. It is similar to the binomial distribution except that the n parameter refers to non-total and incomplete events. In other words, a random variable with NegBinomial distribution of parameters n and p represents the number of successes whose probability is p, which are achieved in a sequence of n failed trials. The parameters by means of which this distribution is defined have the same form as those that represent the Binomial distribution, although, as we said, the parameter n represents a different quality.

Input parameters:

• n. Number of failures until the trial stops, for which it is wanted to find the number of successful trials. This parameter must be an integer greater than zero, although the software will accept positive reals (those will be truncated).
• p. Probability that the trial will be successful. Take real values between 0 and 1.

More help

• Gamma
• Exponential
• Beta
• Poisson
• Binomial
• Von Mises
• Cauchy
• Weibull
• Xi Cuadrado
• LogNormal

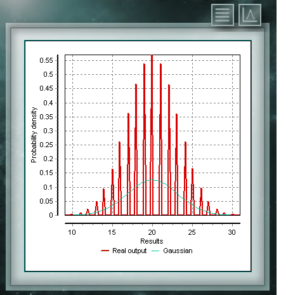Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.

Eingabeparameter:

• n. Anzahl der durchzuführenden unabhängigen Tests. Dieser Parameter muss eine ganze Zahl größer als Null sein.
• p. Wahrscheinlichkeit, dass die Studie erfolgreich sein wird. Nehmen Sie reale Werte zwischen 0 und 1.

More help

• Gamma
• Exponential
• Beta
• Poisson
• NegBinomial
• Von Mises
• Cauchy
• Weibull
• Xi Cuadrado
• LogNormal

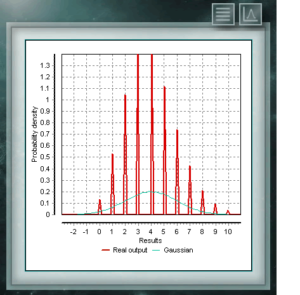The Poisson distribution is a discrete distribution defined for the domain of integers greater than zero. It is used mostly to represent the probability that a certain number of events will occur in a period of time, a defined distance, area, volume, etc.,

Input parameters:

• λ. This parameter greater than zero represents the number of instances in which the phenomenon studied occurs in a given interval. It also represents the mathematical expectation of the random variable.

More help

• Gamma
• Exponential
• Beta
• Binomial
• NegBinomial
• Von Mises
• Cauchy
• Weibull
• Xi Cuadrado
• LogNormal

Beta.

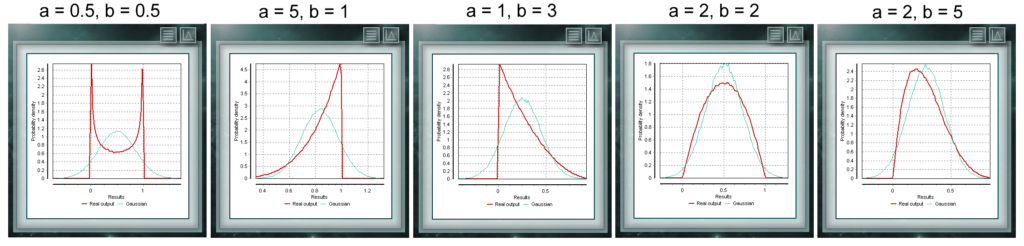This distribution is a continuous function with two parameters which must take real values greater than zero. The function is defined between 0 and 1. A particular case of the Beta distribution is when both form parameters take values = 1. In this case the function will coincide with a uniform distribution.

Input parameters:

• a, b. Shape parameters. They must be both real numbers greater than zero.

More help

• Gamma
• Exponential
• Poisson
• Binomial
• NegBinomial
• Von Mises
• Cauchy
• Weibull
• Xi Cuadrado
• LogNormal

Exponential ditribution.

The exponential probability distribution is a continuous function in the domain of positive reals, which is suitable to represent the time between two events that are distributed according to the Poisson distribution. For example, the elapse until a trade receives its first customer of th day. The exponential distribution is a particular case of the Gamma distribution where shape parameter takes value 1.

Input parameters:

• Mean value. This parameter must be a real number > 0 and defines the position of the mean value of the distribution. Since this is a case of the Gamma distribution, in terms of the latter, the mean would correspond to the Scale parameter if a Gamma with shape = 1 is used. In this case, the resulting probability distribution will be the same.

More help

• Gamma
• Beta
• Poisson
• Binomial
• NegBinomial
• Von Mises
• Cauchy
• Weibull
• Xi Cuadrado
• LogNormal

Gamma distribution.

This distribution is a continuous function of biased character, that is, where the modal value does not correspond to the mean value. The Gamma distribution is a generalization of the exponential distribution, and is used in general to model random variables that represent the time in which an event occurs a certain number of times.

The pseudo-random generated by the application are an approximation (G. Marsaglia and W. Tsang) with a single input parameter called “shape”, which must be a positive real number. From version 3.2 it is possible to describe gamma functions with any standard deviation (using the second parameter named scale).

Input parameters: