When the Start Simulation button is pressed, a bar can be seen under the button that continuously indicates the progress of random sampling. After completing the simulation with the indicated data, the application is automatically located in the results panel.

This panel shows a graphic selector at the top left, which allows to toggle between the results of the Monte Carlo simulation and the analysis according to the GUM approach, which is also estimated as well in all cases.

Next, we analyze the information provided by the MCM results view:

1. Name of the application.
2. Software version.
3. Time involved by the application in obtaining results (in mm.ss, minutes and seconds)
4. Technical data, with the text that we indicated in Step 1
5. Number of iterations. 500 000 in our case.
6. Statistical analysis of simulation
   1. Media = 100.04111
   2. Variance = 1.947357e-4
   3. Standard deviation = 1.39548e-2
   4. Skew = -1.01559e-3
   5. Kurtosis = 2.64392
   6. Maximum value = 100.11192
   7. Minimum value = 99,97472
   8. Median = 100.0396
   9. Range = 0.1372
7. Normality Test (Jarque – Bera) = 2641.5964 (does not fit)
8. Result = 100.04111. This indicates the result of the calibration without rounding figures.
9. Confidence interval (p = 95.45%): [100.01376, 100.06841] (Half-width of the interval = 2.733e-2)
10. Classic format: 100.041 ± 0.027 ml. This represents the test result and its associated expanded uncertainty for the coverage probability indicated in step 3. Note that this is not the result from GUM framework but the MCM results expressed as usual in GUM framework
11. List of contributions to the uncertainty for each parameter of the model.
12. Section with input data and mathematical model describing completely what was entered when creating the simulation project.

More help

• First project – Step 1
• First project – Step 2-A: Basic model
• First project – Step 2-B: Input uncertainties
• First project – Step 2-C: Final model
• First project – Step 3.
• First project – Results

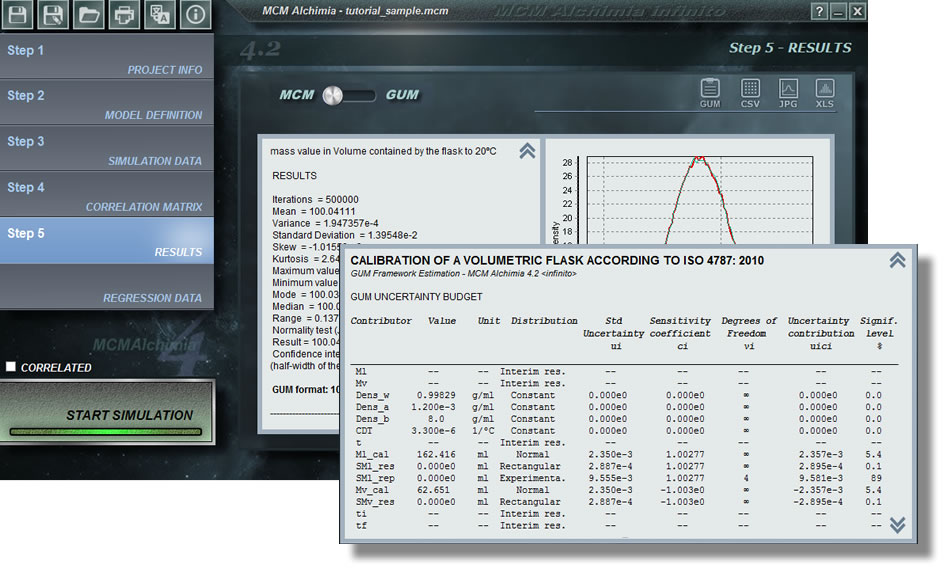
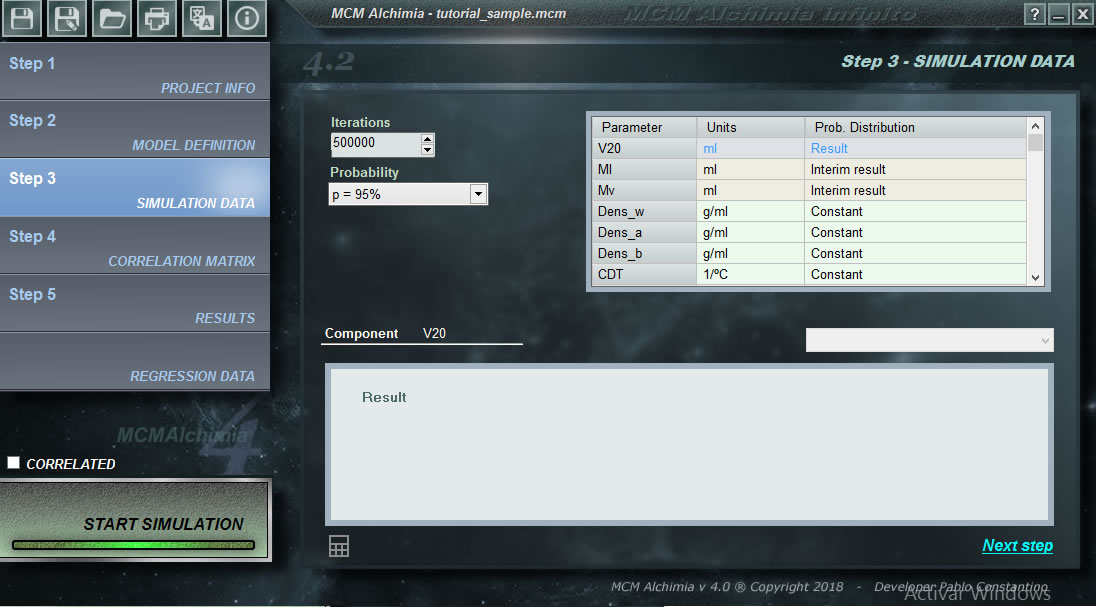
Simulation data

The only thing left for us to do in our first project is to assign a probability distribution function to each random variable that represents our project. As seen in the program, the grid is composed of several rows, some of them with a white background, and others with a gray background. The rows that have a gray background correspond to magnitudes for which a distribution function can not be assigned, because they are intermediate results or the final result, that is, magnitudes that will be obtained in the simulation as a result of secondary equations.

The lower part of the work panel has a command box that will give us a dropdown list of probability distribution functions so that we can select the one that fits the input magnitude. After we have selected a probability distribution, the lower box will ask us to type the necessary parameters to perform the simulation. Therefore the process of this step would be as follows:

1. It is recommended to leave the number of iterations in 500 000 since it is obtained in excellent performance in the application and the results are absolutely reliable with this number of iterations (can be consulted the paper: Computational Aspects in the Estimation of Test Uncertainties by the Monte Carlo Method (Spanish only)
2. We select the probability of coverage for the results. It is recommended to use 95.45% in order to obtain results for K = 2.
3. We click on the first row with white background (or we reach it with the cursor keys of our keyboard)
4. We select a probability distribution function in the drop-down list.
5. We fill the simulation parameters in the lower panel (please, take units into account).
6. We click on Apply. If everything is correct, the row will have a green background, indicating that the magnitude has its simulation data correctly assigned.

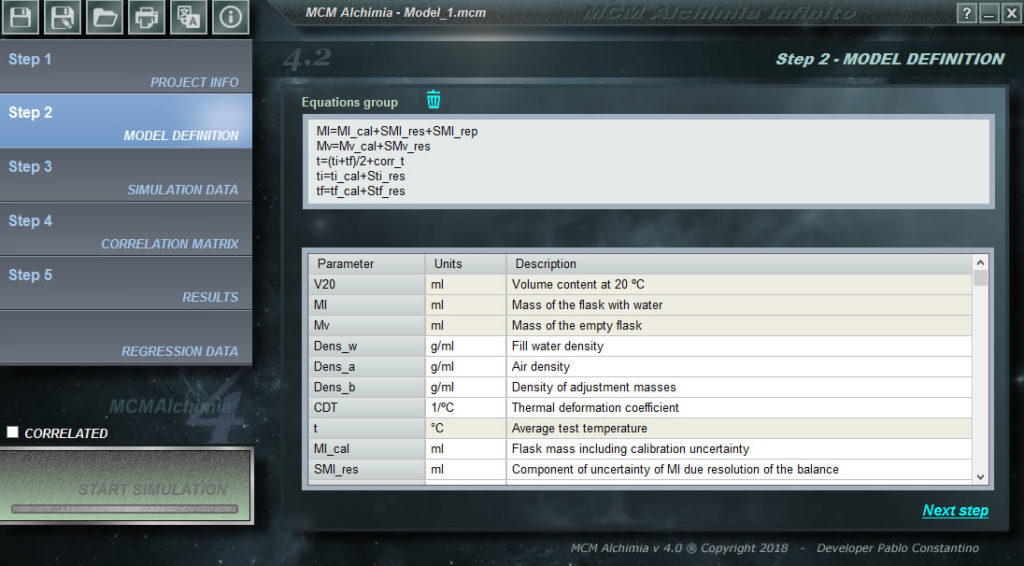
Going back to our volumetric flask we will have so:

1. V20 : Disabled because it is Result, it is not possible to assign an PDF(Probability Distribution Function)
2. Ml : Disabled because it is Intermediate result, It is not possible to assign a PDF
3. Mv : Disabled because it is Intermediate result, It is not possible to assign an PDF
4. Dens_w : We will assign the PDF Constant with a Value = 0.99829 (g / ml)
5. Dens_a : Assign the PDF Constant with a Value = 1.2E-3 (g / ml)
6. Dens_b : We will assign the PDF Constant with a Value = 8,000 (g / ml)
7. CDT : Assign the PDF Constant with Value = 3.3E-6 (1 / ºC)
8. t : Disabled because it is Intermediate result, It is not possible to assign an FDP
9. Ml_cal : Due to an expanded uncertainty, we will assign the PDF Normal with the average value of our readings, Mean = 162,416, entering the certificate information in “Use certificate “, with uncertainty = 0.0047 (g) and k = 2
10. SM_res : We will assign a PDF Rectangular , with Mean = 0 (corresponding to all the variables that are entered only for the purpose of estimating uncertainties) and Half interval = 0.0005 , that is, half of the division of the digital weighing scale.
11. SM_rep : For repeatability, MCM Alchimia provides an experimental PDF where we can directly put the measured values ​​and the application will be responsible for making the statistical calculations necessary for us, to use for simulation. As it is only for uncertainty purposes we will have to select “Force Mean = 0”. We will use the “Direct” option and clicking on the Values ​​button we will enter the 5 readings of our essay: 162,384; 162,431; 162,409; 162.417; 162,439
12. Mv_cal : Due to an expanded uncertainty, we will assign the PDF Normal with a mean in the reading of the balance in order to weigh the empty flask, Mean = 62.651, entering the certificate information in “Use certificate”, with uncertainty = 0.0047 (g) and k = 2
13. SMv_res : We will assign a PDF Rectangular , with Media = 0 and Half interval = 0.0005.
14. ti : Disabled because it is Intermediate result, It is not possible to assign a PDF
15. tf : Disabled because it is Intermediate result, It is not possible to assign a PDF
16. corr_t : We will assign the PDF Constant with Value = -0.022 (ºC)
17. ti_cal : Because it comes from a calibration certificate, we will assign the PDF Normal with the value of our reading of the mean thermometer = 20.05. At the same time we will select “Use certificate” and we will put the expanded uncertainty = 0.021 (ºC) and k = 2.
18. Sti_res : For this measure we use a mercury thermometer in division glass: 0.1ºC, from which we can visually estimate 1/4 of the division. According to this, we will assign a Triangular distribution with Mean = 0 and half-interval = 0.125 (this is estimate / 2)
19. tf_cal : The same is the case as in ti_cal but now our average will be the final temperature: Mean = 20,075, select “Use certificate” and indicate the expanded uncertainty = 0.021 (ºC) and k = 2.
20. Stf_res : Same as Sti_res, that is, Triangular with Media = 0 and semi-interval = 0.125.

When entering data for the last magnitude, the “Run the simulation” button will light up so that we can run our simulation and obtain the results. Watch results after simulation .

More help

• First project – Step 1
• First project – Step 2-A: Basic model
• First project – Step 2-B: Input uncertainties
• First project – Step 2-C: Final model
• First project – Step 3.
• First project – Results.

Determination of the final mathematical model for the test.

In the previous article we saw that our flask calibration test could be represented by the following diagram;

Breaking down the input magnitudes in their contributions we would get:

• Ml = Ml_cal + SMl_res + SMl_rep, where the suffixes “cal”, “res” and “rep” will be by calibration, instrument resolution and repeatability respectively. The prefixes “S” indicate that this component will have zero value since it is added only for the purpose of evaluation of uncertainties.
• Mv = Mv_cal + SMv_res
• The temperature, as we said before will be obtained from an average, so we can break down the equation in this average of readings. On the other hand, this thermometer has corrections. We could add this correction value (corr_t) to the average as a constant value without uncertainty, since this will be associated to the original values ​​of temperature.
  t = (ti + tf) / 2 + corr_t
• but each one of these values ​​will be affected by the calibration and resolution of the thermometer. So:
  ti = ti_cal + Sti_res
  tf = tf_cal + Stf_res

Therefore to conclude this step 2:

1. We write the complete model in the text area for the Set of equations:
   V20 = ((Ml-Mv) / (Dens_w-Dens_a)) * (1- (Dens_a / Dens_b)) * (1-CDT * (t-20))
   Ml = Ml_cal + SMl_res + SMl_rep
   Mv = Mv_cal + SMv_res
   t = (ti + tf) / 2 + corr_t
   ti = ti_cal + Sti_res
   tf = tf_cal + Stf_res
2. We fill the parameters grid with the following data:

More help

• First project – Step 1
• First project – Step 2-A: Basic model
• First project – Step 2-B: Input uncertainties
• First project – Step 2-C: Final model
• First project – Step 3.
• First project – Results.

Analysis of input values and their uncertainties

At this stage it is advisable to analyze the magnitudes that make up the input model to determine the contributions of uncertainty that they contribute. The advisable thing in this case is to define a model that represents as faithfully as possible the development of our analysis or trial, so that the contributions of uncertainty are adjusted to those that will really represent the model. Although we will then propose a way to do it, it is understood that each expert will do it in their own way and, therefore, the different processes will involve different final mathematical models for the trial. It is not the purpose of this aid the background discussion on volume metrology but for a given test model, finding a way to represent it faithfully.

Thus, we are assuming for our analysis that the characteristics of the test will be:

• The flask is initially washed, dried in an oven, allowed to cool and weighed once at 20 ° C on a digital scale. This magnitude, then, will mean contributions of uncertainty for the calibration of the balance
• The mass of the flask filled with water will be determined by repeating 5 times the measurement, weighing on a calibrated scale. Therefore this magnitude will bring uncertainty due to the calibration of the scale, its resolution and the repeatability of the measurement.
• The temperature of the test water will be taken at the beginning and at the end of the test with a mercury glass thermometer, the average of these two measurements being used for the calculation. The contributions will then be for the calibration of the thermometer, the division thereof and for the drift found in the measurement throughout the test.
• The other magnitudes (densities and coefficient of expansion) will be taken from tables and will be assumed constant in this opportunity (without contribution of uncertainty)

Therefore, the Cause-Effect diagram (Ishikawa) for our essay will be:

To write the complete model, then you should break down the basic magnitudes in their components, adding new lines to the model. This will be discussed in the next stage by clicking this link .

More help

• First project – Step 1
• First project – Step 2-A: Basic model
• First project – Step 2-B: Input uncertainties
• First project – Step 2-C: Final model
• First project – Step 3.
• First project – Results.