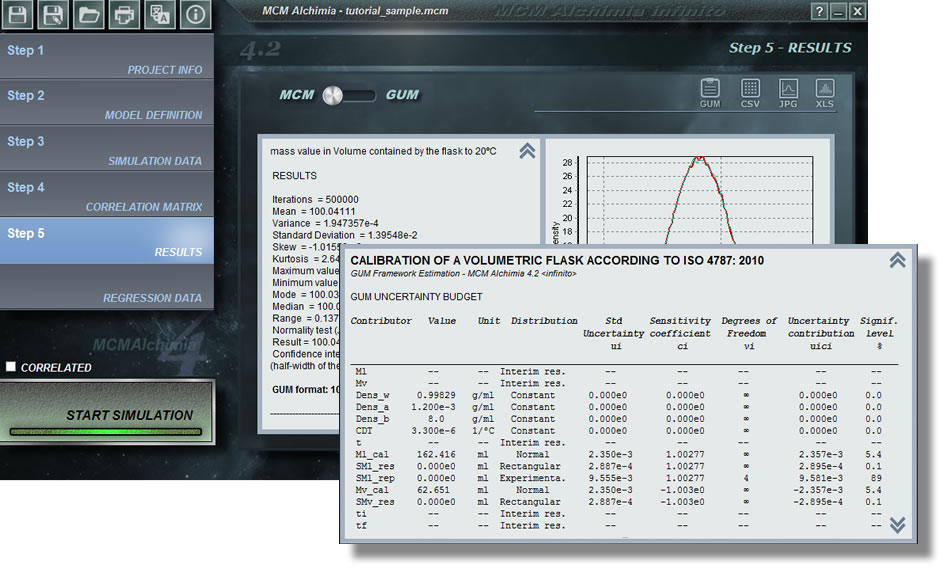
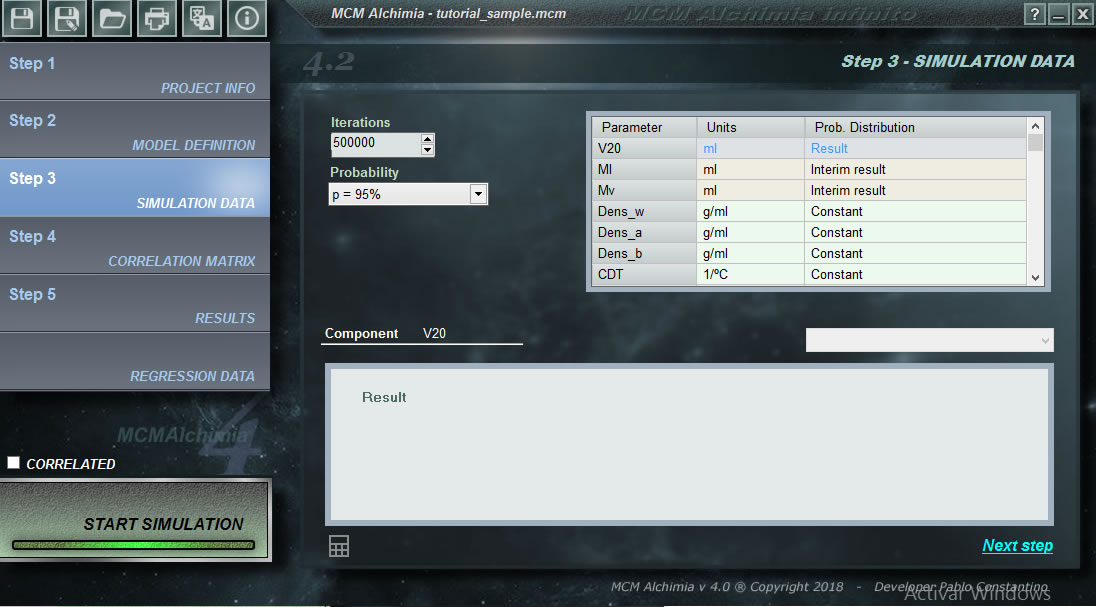
Während MCM Alchimia in jedem Bereich verwendet werden kann, der Monte-Carlo-Simulationen erfordert, wurde das Tool unter Berücksichtigung der Messunsicherheitsanalyse entwickelt. Aus diesem Grund sind viele der vordefinierten Optionen in dieser Software einzigartig und werden nicht in ähnlichen Anwendungen gefunden (experimentelle Verteilung, Analyse von Kalibrierungskurven oder das Ergebnis im klassischen GUM-Format gemäß JCGM 100). Im Folgenden geben wir einige Tipps und Tricks für Sie, um ein Experte in der Anwendung der Anwendung zu werden und in kürzester Zeit zuverlässigere und schnellere Ergebnisse zu ermöglichen.
1 .- Empfohlene Arbeitsreihenfolge
Während die Anwendung sehr intuitiv ist, ist es immer gut, einer Arbeitsfolge zu folgen, um sowohl die Genauigkeit der Berechnungen als auch die Effizienz bei der Verwendung der Zeit sicherzustellen. Die Methodik der Arbeit kann in den folgenden Phasen zusammengefasst werden.
- Definition des mathematischen Modells der Messgröße. In dieser Phase wird das Grundmodell (Gleichung) unseres Versuchs definiert, so wie wir normalerweise die Berechnungen durchführen, oder wie es in unseren Referenzdokumenten empfohlen wird.
- Die Aufschlüsselung der Eingangsgrößen in Quellen der Unsicherheit. Es ist notwendig, alle Quellen der Unsicherheit zu bewerten, aus denen sich jede Eingangsmenge zusammensetzt. Zum Beispiel werden bei der Verwendung eines Messinstruments mindestens zwei Unsicherheitsquellen gefunden, eine aufgrund der Kalibrierung und eine andere aufgrund der Auflösung (oder Unterteilung) des Geräts. Es kann aber auch Steuerzahler für zusätzliche Bewertungen geben (z. B. Wiederholbarkeit). Wir empfehlen ein Ursache-Wirkungs-Diagramm, um die Steuerzahler des Modells allgemein zu sehen.
- Schreiben Sie für jede Größe des Basismodells, das mehr als eine Unsicherheitsquelle aufweist, eine zusätzliche Gleichung in nachfolgende Zeilen. Verwenden Sie das Präfix „S“ für die Komponenten, die Wert = 0 annehmen und nur durch die Unsicherheit berücksichtigt werden. Dies wird am besten im nächsten Punkt erklärt.
- Überprüfen Sie, dass in jeder geschriebenen Gleichung die Anzahl der öffnenden Klammern gleich der Anzahl der runden Klammern ist.
- Es ist praktisch, vor dem Zuweisen der Werte und Verteilungen eine Tabelle auf Papier mit den Spalten zu erstellen:
Variable / Einheiten / Wert (Mittelwert) / Wahrscheinlichkeitsverteilung / Standarabweichung (oder Semi-Intervall).
Dies ermöglicht es, alle Komponenten in der Allgemeingültigkeit des Modells zu sehen. Diese Daten werden dann in Schritt 3 eingegeben.
- Wenn Sie diese Schritte befolgen, ist Ihr Erfolg sicher. Denken Sie daran, dass die Verwendung von Zeit in Ihrem Projekt zu 80% dem korrekten Entwurf des mathematischen Modells (der Testgleichung) gewidmet ist.
2 .- Empfohlene Arbeitssequenz
Der leistungsstarke Formeleditor von MCM Alchimia ermöglicht es Ihnen, eine unbegrenzte Anzahl von Gleichungen im Textbereich zu schreiben. Es ist nicht notwendig, das gesamte mathematische Modell des Essays in einer einzigen Zeile zu schreiben. Um zu vermeiden, dass Fehler am Klammergleichgewicht oder andere am Ende schwer zu finden sind, empfiehlt es sich, mit einem Basismodell zu beginnen, das allgemeine Variablen enthält, und dann spezifische Gleichungen für jede Basisgröße zu schreiben. Sie können das Beispiel eines gelösten Modells sehen, später in der Hilfe, die auf diese Weise gemacht wird.
3. Regeln für den Formeleditor
Obwohl es möglich ist, jedes Modell mit MCM Alchimia darzustellen, hat der Gleichungseditor einige Regeln, an die man sich gut erinnern sollte, um Fehler zu vermeiden.
- Alle Gleichungen müssen im Format [measurand] = f ([Variable 1] [Variable 2] … [Variable n]) geschrieben sein, dh beide Elemente der Gleichung müssen enthalten sein.
- Es kann nur eine Größenordnung der Ausgabe im Modell (Messgröße) geben
- Die Ausgabegröße muss in der ersten Zeile stehen
- Es ist nicht erlaubt „;“ Am Ende der Zeile genügt der Wagenrücklauf (Enter) am Ende der Zeile, um die Gleichungen zu trennen
- Es ist nicht erlaubt, zwei Gleichungen mit demselben Zwischenergebnis einzugeben.
- Der Editor erlaubt ASCII-Zeichen (Großbuchstaben, Kleinbuchstaben, Zahlen und Unterzeichen und Sonderzeichen der virtuellen Tastatur, die mit der Schaltfläche αβ angezeigt werden können). Beispiele für Variablennamen können sein „Vol_p“, „Temp2“, „δ_724“, „Δt“ usw. Variablennamen wie „2_t“ (nach Nummer bei Start) oder „ABS“ (da es sich um einen eingeschränkten Begriff handelt, ist eine Funktion) sind nicht erlaubt )
- Variablennamen müssen mit einem alphabetischen Zeichen beginnen und außerdem können Zahlen nicht am Anfang des Namens verwendet werden.
- Bei Variablennamen wird zwischen Groß- und Kleinschreibung unterschieden.
- Es gibt reservierte Begriffe, die Funktionen entsprechen, die nicht als Variablennamen verwendet werden können.
- Die Verknüpfung f(s) m Bereich der Gleichungen öffnet eine Tastatur mit Funktionen, die direkt im Modell verwendet werden können. Wenn ein Teil der Gleichung markiert ist und dann eine Funktion mit der Tastatur ausgewählt wird, bleibt dieser Teil der Gleichung als Parameter der Funktion erhalten.
- Eine Verknüpfung mit griechischen Buchstaben ist ebenfalls verfügbar, die es erlaubt, Zeichen aus dem griechischen Alphabet in Variablennamen einzufügen.
4 .- Wie man Variablen mit verschiedenen Quellen der Unsicherheit einbezieht
Ein sehr häufiger Fall in Tests und Kalibrierungen ist, dass die Größen mehr als eine Unsicherheitsquelle haben. Zum Beispiel kann die Verwendung eines Messinstruments aufgrund seiner Kalibrierung, Auflösung, Wiederholbarkeit usw. mehrere Unsicherheitsbeiträge liefern. Um all diese Quellen der Unsicherheit zu umfassen, gibt es zwei Möglichkeiten, um fortzufahren:
- Die Größenordnung kann in so viele Summanden wie Quellen der Unsicherheit unterteilt werden. Die erste wird den gemessenen oder gelesenen Wert (als Durchschnitt) annehmen, und der Rest wird eine zentrierte Verteilung sein (Durchschnittswert = 0), da sie nur zur Bewertung der Unsicherheit verwendet werden und das Ergebnis nicht beeinflussen werden. Z.B. Eine 10-fache Temperatur, die Unsicherheiten für Kalibrierung, Auflösung und Wiederholbarkeit liefert, kann ausgedrückt werden als:
T = T_cal + ST_res + ST_REP.
- Die andere Möglichkeit besteht darin, die Größe in eine Konstante und dann in die Unsicherheitsbeiträge aufzuteilen, alle mit einem Durchschnittswert = 0. Dem vorherigen Beispiel folgend wäre:
T = T_Wert + ST_cal + ST_res + ST_Rep
Beachten Sie, dass die Variablen für die Unsicherheit, die einen Nullwert annehmen, mit einem Anfangs-S geschrieben wurden. Obwohl sie einen beliebigen Namen annehmen können, ist es eine gute Vorgehensweise, Namen mit einem gemeinsamen Kriterium wie diesem zu unterscheiden. Auf diese Weise kann die Struktur des Modells bereits aus dem Namen der Variablen bekannt sein.
5 .- Geben Sie A-Unsicherheiten mit MCM Alchimia ein
Ein sehr häufiger Fehler bei der Verwendung der Monte-Carlo-Methode zur Schätzung von Unsicherheiten ist die Zuordnung der Normalen Verteilungsfunktion zu den Größen, die „Typ A“ Unsicherheiten darstellen, wobei als Standardabweichung die Standardabweichung der Messwerte.
Dies führt zu falschen Unsicherheitsresultaten (Unterschätzungen) aufgrund der Tatsache, dass wenig Information über die Population berücksichtigt wird, das heißt die „Freiheitsgrade“, wie sie im GUM-Ansatz verwendet werden. Wenn man die berechnete Standardabweichung direkt annimmt, nimmt man an, dass diese Größe unendlich viele Freiheitsgrade hat, was nicht korrekt ist.
Es gibt drei Möglichkeiten, korrekt Typ-A-Unsicherheiten in MCM Alchimia einzubeziehen
- Die JCGM 101 Auswertung des Messdatenleitfadens – Ergänzung 1 zum. „Leitfaden für den Ausdruck der Unsicherheit in der Messung“ zeigt an, dass für Typ-A-Unsicherheiten eine Student-t-Verteilung (skaliert und verschoben) statt einer Gaußschen verwendet werden sollte. Für diese Verteilung sollte als Parameter die Freiheitsgrade angegeben werden, damit das Informationsniveau, das Sie von der Größe haben, enthalten ist.
- Falls Sie die Normalverteilung verwenden möchten, können Sie das auch tun, obwohl als Standardabweichung die in unserem Test berechnete Abweichung eingegeben werden sollte, multipliziert mit dem Deckungsfaktor für unsere Freiheitsgrade und 95.45% Abdeckungswahrscheinlichkeit ( inverse t-Verteilung), geteilt 2. Diese einfache Operation erlaubt die Simulation unter Berücksichtigung der Freiheitsgrade der Magnitude.
- Unsere Empfehlung. Eine exklusive Spezifikation von MCM Infinite Alchimia, ist die Einbeziehung eines FDP namens Experimental. Dieses leistungsstarke Panel ermöglicht es uns, mit Typ-A-Unsicherheiten direkt aus den Rohwerten unseres Tests zu arbeiten, ohne dass wir irgendeine Standardabweichung oder andere Operationen berechnen müssen. Mit dieser Option wird die Anwendung automatisch das Problem der Freiheitsgrade, Standardabweichungen usw. behandeln. Sie können sogar für komplexere Wiederholbarkeitsmodelle verwendet werden, für Sample / Standard / Sample und andere.
Mehr Hilfe
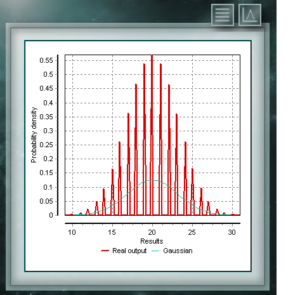Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.
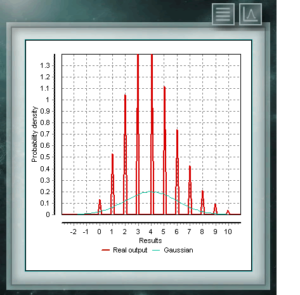Die Poisson-Verteilung ist eine diskrete Verteilung, die für die Domäne von Ganzzahlen größer als Null definiert ist. Sie wird meistens verwendet, um die Wahrscheinlichkeit darzustellen, dass eine bestimmte Anzahl von Ereignissen in einem bestimmten Zeitraum, einer definierten Entfernung, Fläche, Volumen usw. auftritt.
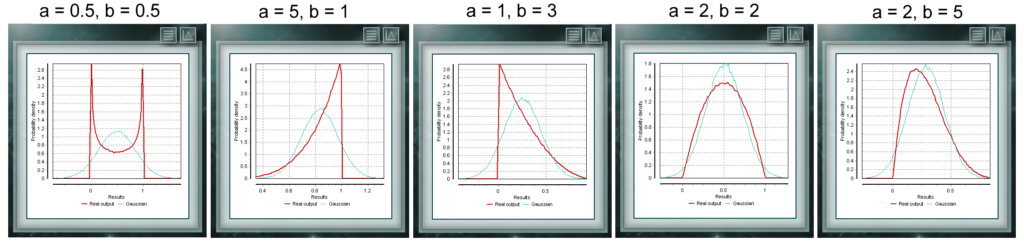Diese Verteilung ist eine stetige Funktion mit zwei Parametern, die reale Werte größer als Null annehmen müssen. Die Funktion ist zwischen 0 und 1 definiert. Ein besonderer Fall der Beta-Verteilung liegt vor, wenn beide Formularparameter Werte = 1 annehmen. In diesem Fall fällt die Funktion mit einer gleichmäßigen Verteilung zusammen.
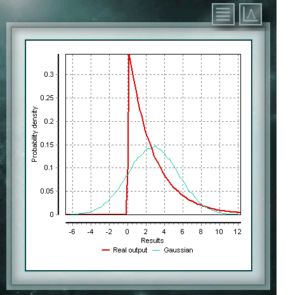Die exponentielle Wahrscheinlichkeitsverteilung ist eine stetige Funktion im Bereich der positiven Realen, die geeignet ist, die Zeit zwischen zwei Ereignissen darzustellen, die gemäß der Poissonverteilung verteilt sind. Zum Beispiel, bis der Handel seinen ersten Kunden des Tages erhält. Die Exponentialverteilung ist ein besonderer Fall der Gamma-Verteilung, bei der der Formparameter den Wert 1 annimmt.
Diese Verteilung ist eine fortlaufende Funktion von Vorurteilen, d. H. Wenn der modale Wert nicht dem Mittelwert entspricht. Die Gamma-Verteilung ist eine Verallgemeinerung der Exponentialverteilung und wird im Allgemeinen zum Modellieren von Zufallsvariablen verwendet, die die Zeit darstellen, zu der ein Ereignis eine bestimmte Anzahl von Malen auftritt.
