 Zum Öffnen der Funktionstastatur klicken Sie auf den Link f(x) , der sich im Gleichungseditor befindet, wenn Sie uns darauf positionieren.
Zum Öffnen der Funktionstastatur klicken Sie auf den Link f(x) , der sich im Gleichungseditor befindet, wenn Sie uns darauf positionieren.
Im unteren Bereich der Funktionstastatur befinden sich zwei Interpolationsschaltflächen, mit denen Sie lineare Interpolationsergebnisse in der verbundenen Kurve erhalten können. Diese generischen Variablen führen nicht nur die Interpolation in der Kurve durch, sondern führen auch die Abschätzung der Unsicherheit durch, indem sie ihren Beitrag zum Modell integrieren.
Es ist wichtig zu verstehen, dass diese Berechnung nicht das darstellt, was normalerweise manuell durchgeführt wird, sondern alle in der Simulation des Modells verfügbaren Werkzeuge sowie die Daten, die während der Simulation der verbundenen Kurve erhalten werden.
REG_y (x). Interpoliert die beobachtete Antwort ( y ) eines angezeigten Werts von der x -Achse und schätzt die damit verbundene Gesamtunsicherheit. Der Wert von x kann numerisch sein, eine Variable oder sogar ein Teil der Modellgleichung. Zum Beispiel REG_y (5), REG_y (A) oder REG_y (coef_a * ABS (A1-A2)).
REG_x (y). Bei einem Wert, einer Variablen oder einem Fragment der Gleichung, die der y -Achse entspricht, interpolieren und schätzen Sie die zugehörige Unsicherheit des entsprechenden Werts von x .
Unsicherheit der Interpolation.
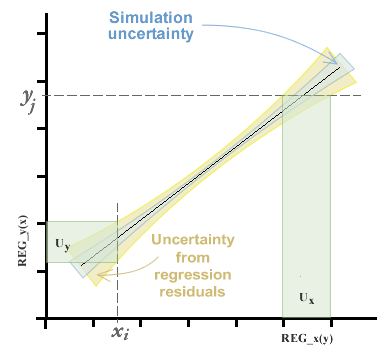
Im Kapitel Verwenden des Kalibrierungskurvenfelds haben wir gesehen, dass wir schätzen können die Kurve der besten Anpassung durch die Methode der gewöhnlichen, inversen und der Summe der kleinsten Quadrate (letztere mittels der Analysemethode der Hauptkomponente). Welche Methode auch immer gewählt wird, wir erhalten Koeffizienten der Geradengleichung zusätzlich zu einem Bereich variabler Unsicherheit entlang der Kurve, der sich aus der Unsicherheit der Simulation zusammensetzt und der durch die Varianz der Residuen beigetragen wird. Dieses Thema wird im Kapitel über Regressionen und Kurven ausführlicher behandelt.
Die Unsicherheit bei der Interpolation wird dann durch den Standardfehler der Kurve in der Achse angegeben, von der sie zu interpolieren beabsichtigt.
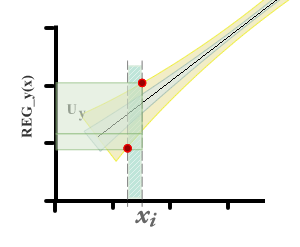
Es ist ersichtlich, dass es zwei Unterschiede in Bezug auf das Verfahren gibt, das üblicherweise zum Schätzen der Unsicherheit in Kalibrierungskurven verwendet wird. Erstens wird auf der x -Achse keine Nullunsicherheit erwartet.
Wenn Sie dagegen den Wert von x i aus einem y i

