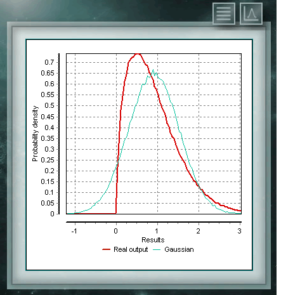
Diese Verteilung ist eine kontinuierliche Funktion im Bereich positiver reeller Zahlen, die häufig in der Volkswirtschaftslehre, der Meteorologie und der Telekommunikation verwendet werden, sowie in anderen spezifischen Anwendungen, wie der Zuverlässigkeitsrate oder dem Überleben von Organismen oder Maschinen. Die Zufallsvariablen, die das Weibull-Verteilungsmodell haben, sind die Verteilung von Fehlern in Systemen, wenn die Fehlerquote proportional zur Zeitstärke ist. Diese Verteilung wird aus einem charakteristischen Form (& gt; 0) -Parameter definiert, der die Ausfallrate anzeigen würde. Wenn die Ausfallrate abnimmt, ist sie konstant oder steigt mit der Zeit an. Dies entspricht, wenn der Parameter k kleiner, gleich oder größer als 1 ist.
Eingabeparameter:
- Form. Dieser Parameter definiert die Form der Verteilung. Sie können eine beliebige Feldnummer von reellen Zahlen als Null annehmen.
- Skalieren. Dieser zweite Parameter ermöglicht die Skalierung der resultierenden Werte, wobei Pseudozufallszahlen mit derselben Form erzeugt werden, jedoch mit einer größeren Standardabweichung.
Mehr Hilfe
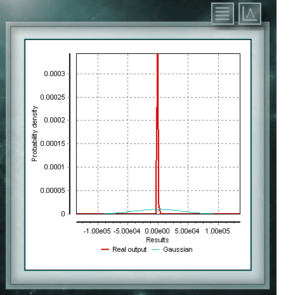Die Cauchy-Verteilung hat die Besonderheit, dass sie vom Gaußschen Verteilungstyp ist, jedoch hat sie den höchsten Peak und die Schwänze zerfallen sehr langsam. Obwohl MCM Alchimia in geeigneter Weise die Pseudo-Zufalls-Abtastwerte für diese Verteilung erzeugt, wird der Ergebnisgraph wie ein isolierter Peak aussehen, da die Abszissenachse im 99% igen Wahrscheinlichkeitsintervall der Abdeckung liegt. Da der Zerfall der Schwänze so graduell ist, wird der Bereich signifikanter Wahrscheinlichkeiten sehr eng.
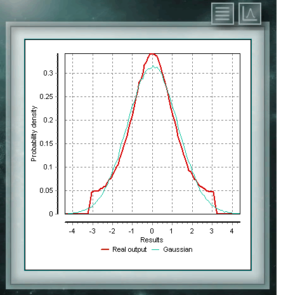Die Verteilung von Von Mises ist eine kontinuierliche Funktion der zirkularen Aufrufe, dh sie sind für die realen im Intervall von 0 bis 2p definiert. Diese Funktion wird derzeit vorzugsweise auf dem Gebiet der Epidemiologie verwendet, um die Ausbreitung von Krankheiten oder technologischen Anwendungen wie der Signalverarbeitung zu beschreiben. Die Von-Mises-Verteilung wird auch als normaler Kreis bezeichnet, da sie dem Gaußschen ähnelt, jedoch auf die Kreisebene beschränkt ist.
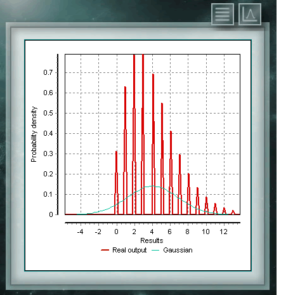Die NegBinomialverteilung ist auch eine diskrete Verteilung, die im Bereich positiver Ganzzahlen definiert ist. Sie ist der Binomialverteilung ähnlich, mit der Ausnahme, dass sich der Parameter n auf nicht vollständige und unvollständige Ereignisse bezieht. Mit anderen Worten, eine Zufallsvariable mit NegBinomialverteilung der Parameter n und p stellt die Anzahl der Erfolge dar, deren Wahrscheinlichkeit p ist, die in einer Folge von n fehlgeschlagenen Versuchen erreicht werden. Die Parameter, über die diese Verteilung definiert wird, haben dieselbe Form wie diejenigen, die die Binomialverteilung repräsentieren, obwohl der Parameter n, wie gesagt, eine andere Qualität darstellt.
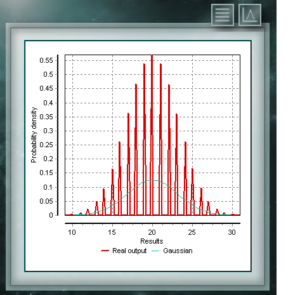Dies ist eine diskrete Verteilung, deren Domäne die Menge positiver Ganzzahlen ist, die die Anzahl der in einer Folge von n Versuchen erzielten Erfolge darstellt. Diese Tests müssen dichotom sein, dh sie bieten nur zwei Möglichkeiten (Erfolg und Misserfolg) und haben eine definierte Erfolgswahrscheinlichkeit = p.
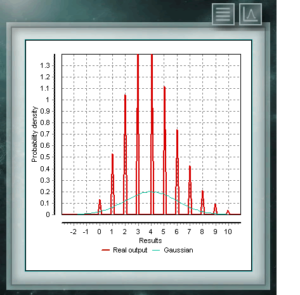Die Poisson-Verteilung ist eine diskrete Verteilung, die für die Domäne von Ganzzahlen größer als Null definiert ist. Sie wird meistens verwendet, um die Wahrscheinlichkeit darzustellen, dass eine bestimmte Anzahl von Ereignissen in einem bestimmten Zeitraum, einer definierten Entfernung, Fläche, Volumen usw. auftritt.
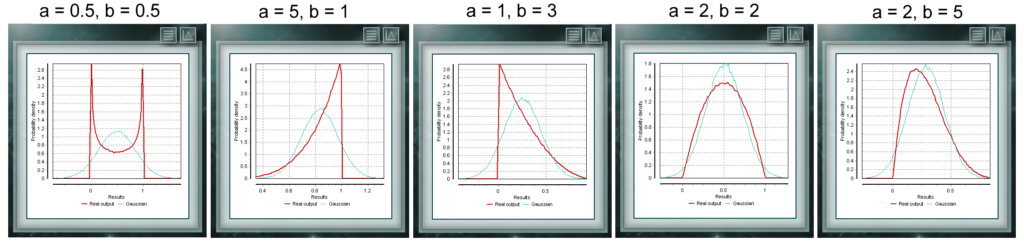Diese Verteilung ist eine stetige Funktion mit zwei Parametern, die reale Werte größer als Null annehmen müssen. Die Funktion ist zwischen 0 und 1 definiert. Ein besonderer Fall der Beta-Verteilung liegt vor, wenn beide Formularparameter Werte = 1 annehmen. In diesem Fall fällt die Funktion mit einer gleichmäßigen Verteilung zusammen.
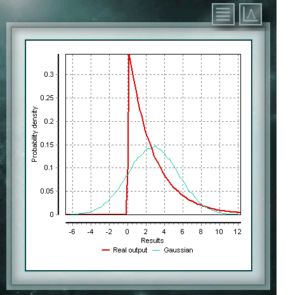Die exponentielle Wahrscheinlichkeitsverteilung ist eine stetige Funktion im Bereich der positiven Realen, die geeignet ist, die Zeit zwischen zwei Ereignissen darzustellen, die gemäß der Poissonverteilung verteilt sind. Zum Beispiel, bis der Handel seinen ersten Kunden des Tages erhält. Die Exponentialverteilung ist ein besonderer Fall der Gamma-Verteilung, bei der der Formparameter den Wert 1 annimmt.
Diese Verteilung ist eine fortlaufende Funktion von Vorurteilen, d. H. Wenn der modale Wert nicht dem Mittelwert entspricht. Die Gamma-Verteilung ist eine Verallgemeinerung der Exponentialverteilung und wird im Allgemeinen zum Modellieren von Zufallsvariablen verwendet, die die Zeit darstellen, zu der ein Ereignis eine bestimmte Anzahl von Malen auftritt.