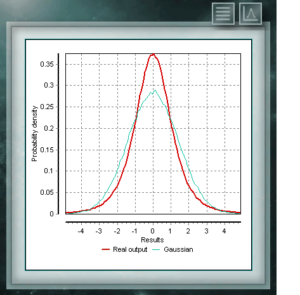
Es ist üblich, bei allen Arten von Analysen, Tests oder Kalibrierungen davon auszugehen, dass sich wiederholende Ereignisse ohne externe Stimuli, die ihre Wahrscheinlichkeiten variieren, gemäß einer durch den Mittelwert definierten Normal- oder Gaußverteilung verteilt werden und die für die Probe berechnete Standardabweichung. Genau genommen trifft dies nur zu, wenn die Anzahl der Wiederholungen groß ist, was mit dem zentralen Grenzwertsatz übereinstimmt. Wenn wir jedoch nicht über ausreichende Informationen verfügen, um die Eigenschaften dieser Gaußschen Verteilung zu beschreiben, weil unsere Untersuchungsstichprobe nicht groß genug ist, nehmen Sie diese Bedingungen an erfüllt sind, werden wir die für unsere Messung unterschätzten Unsicherheitswerte, wie im Leitfaden JCGM 100 – Leitfaden zum Ausdruck der Unsicherheit bei der Messung angegeben, sicherlich überschreiten.
Das gleiche Problem wurde von William Gosset angesprochen, der aus Gründen des Geschäftsgeheimnisses des Unternehmens, in dem er arbeitete, seine Arbeit als „Student“ unterschrieb. Gosset musste aus experimentellen Daten eine Verteilung schätzen, die kleine Proben unbekannter Varianz repräsentierte. Diese von Gosset vorgeschlagene Verteilungsfunktion ist als Student t-Verteilung bekannt und reagiert auf die folgende allgemeine Gleichung:
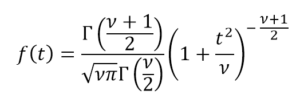
In jeder normalverteilten Grundgesamtheit ermöglicht die Student t-Verteilung die Vergrößerung der Breite der resultierenden Normalverteilung, um die mit der Messgröße verbundene Unsicherheit infolge der Informationsarmut zu erhöhen, die eine kleine Stichprobe des gesamten Loses liefert. In dem Maße, in dem diese Probe größer ist, nähert sich die Verteilung t der Normalen an, die sich aus der Standardabweichung der Probe ergeben, bis sie für unendliche Wiederholungen des Ereignisses mit dieser identisch ist.
Bei allen Arten von Analysen ist es richtig, den sich wiederholenden Ereignissen die Verteilung t mit einem Parameter gl zuzuordnen, der die Freiheitsgrade ist, deren Wert die Anzahl der Wiederholungen minus 1 ist. MCM Alchimia ermöglicht die Simulation einer Zufallsauswahl entsprechend bei der Student t-Verteilung nicht nur mit diesem Parameter der Form (Freiheitsgrade), sondern auch mit Parametern von Skalierung und Position durch die Standardabweichung bzw. den Mittelwert, so dass sie in jeder Situation, wo angemessen, mit Nein verwendet werden kann zusätzliche Operationen.
Eingabeparameter:
- Mittelwert. Dieser Parameter definiert die Verschiebung der Funktion auf der Abszissenachse. Entspricht dem Durchschnittswert der Zufallsvariablen. Die Datensammlung dieser Variablen wird daher auf beiden Seiten dieser Funktion verteilt. Bei dieser Verteilung fällt der Durchschnitt wie bei allen symmetrischen Funktionen mit dem statistischen Modus zusammen.
- Freiheitsgrade. Entspricht der Anzahl der Wiederholungen minus 1. Stellt die Anzahl der Werte dar, die variieren können, ohne den Wert des Stichprobenmittelwerts zu ändern.
- Standardabweichung. Maß der Streuung der Werte in Bezug auf den Probenmittelwert. Wenn diese Verteilung für (statistische) Unsicherheitskomponenten vom Typ A verwendet wird, kann dieser Wert gemäß der folgenden Gleichung berechnet werden:
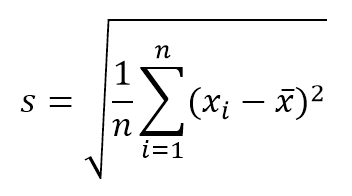
Dabei ist n die Anzahl der Werte oder Wiederholungen. Wenn Sie dagegen die Standardabweichung der Stichprobenmittel kennen möchten, erhalten Sie diesen Wert durch Teilen von s / √ n .
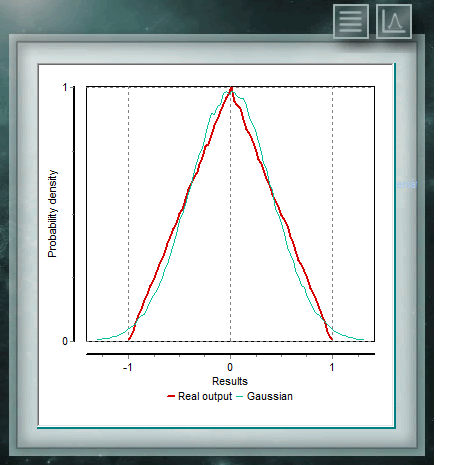Die durchgehende Dreiecksverteilung ist dadurch gekennzeichnet, dass sie wie im Fall des Rechtecks an zwei Extreme begrenzt ist, aber auch einen Modus (oder einen wahrscheinlicheren Wert) innerhalb dieses Bereichs aufweist. Die Wahrscheinlichkeit in jedem Teilintervall gleicher Länge steigt linear bis zur Art und Weise und fällt dann auf die gleiche Weise bis zur oberen Grenze ab. Diese Verteilung wird häufig in Variablen verwendet, bei denen die Informationen begrenzt sind, wie im Fall der Uniform, bei denen jedoch eine ungefähre Kenntnis des Modalwerts vorliegt, d. H. Wo der genaue Punkt dieses Wertes nicht bekannt ist, jedoch Informationen vorhanden sind der Region oder des Teilintervalls, wo sie zu finden sind.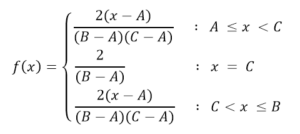
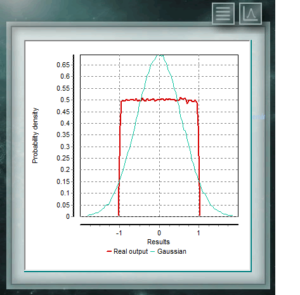Diese kontinuierliche Verteilung ist dadurch gekennzeichnet, dass sie für jeden Wert des Intervalls die gleiche Wahrscheinlichkeit hat. Es wird häufig für Beiträge von Typ-B-Unsicherheiten verwendet, bei denen nur die Haupt- und Nebenabmessungen des Intervalls bekannt sind, beispielsweise in der Aufteilung oder Auflösung eines digitalen Instruments. In vielen Fällen kann diese Verteilung auch zugeordnet werden, wenn wenig Informationen über die Zufallsvariable, in bibliographischen Daten vorhanden sind oder wenn der Überdeckungsfaktor einer Unsicherheit nicht bekannt ist.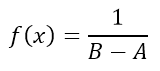
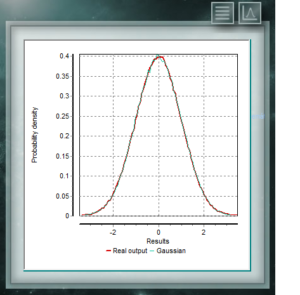Diese Verteilung ist diejenige, die am häufigsten natürliche und soziale Ereignisse darstellt. Die meisten Beweise aus der klassischen Statistik sowie die Abschätzung von Unsicherheiten beruhen auf der Annahme, dass die Daten einer Normalverteilung entsprechen. Aus theoretischer Sicht behauptet der zentrale Grenzwertsatz, dass bei einer ausreichend großen Stichprobe die Verteilung der Mittel einer annähernd Normalverteilung folgt. Die allgemeine Formel dieser Verteilung lautet: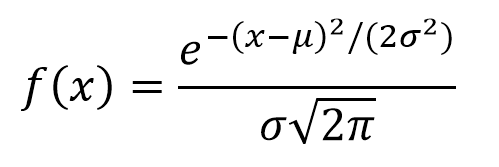
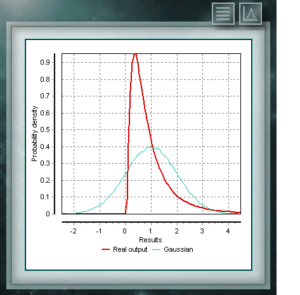Diese Verteilung stellt Zufallsvariablen dar, deren Logarithmen gemäß einer Normalverteilung verteilt sind. Die logarithmische Normalverteilung nimmt abhängig vom Wert ihres Skalenparameters unterschiedliche Formen an und wird häufig in der Zuverlässigkeit von Hochtechnologieprodukten und auch in mikrobiologischen Zählungen verwendet, da sie auf dem multiplikativen Wachstumsmodell basieren.
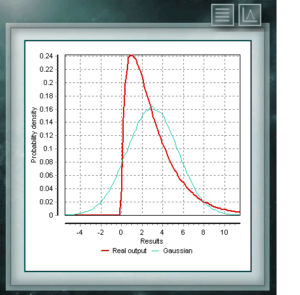Diese kontinuierliche Wahrscheinlichkeitsverteilung im Bereich der positiven Realen steht in engem Zusammenhang mit der Normalverteilung, zum Beispiel ist sie die Stichprobenverteilung von σ². Die Chi Ssquare-Verteilung wird mit einem einzigen Parameter definiert, bei dem es sich um Freiheitsgrade handelt. Die Funktion ist immer asymmetrisch und nach rechts geneigt. Diese Verteilung wird in verschiedenen Bereichen der Wissenschaft sehr häufig verwendet, da sie die Analyse von Datensätzen ermöglicht und bestimmt, ob der Unterschied zwischen ihnen durch Zufall (Nullhypothese) oder durch einen anderen externen Faktor bedingt ist.
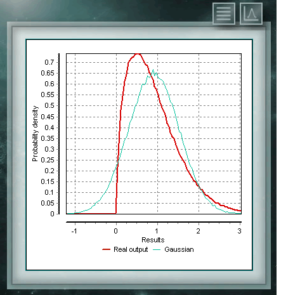Diese Verteilung ist eine kontinuierliche Funktion im Bereich positiver reeller Zahlen, die häufig in der Volkswirtschaftslehre, der Meteorologie und der Telekommunikation verwendet werden, sowie in anderen spezifischen Anwendungen, wie der Zuverlässigkeitsrate oder dem Überleben von Organismen oder Maschinen. Die Zufallsvariablen, die das Weibull-Verteilungsmodell haben, sind die Verteilung von Fehlern in Systemen, wenn die Fehlerquote proportional zur Zeitstärke ist. Diese Verteilung wird aus einem charakteristischen Form (& gt; 0) -Parameter definiert, der die Ausfallrate anzeigen würde. Wenn die Ausfallrate abnimmt, ist sie konstant oder steigt mit der Zeit an. Dies entspricht, wenn der Parameter k kleiner, gleich oder größer als 1 ist.
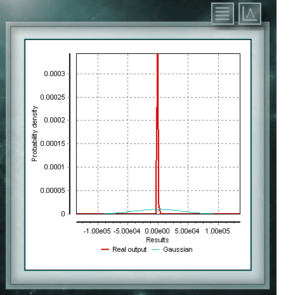Die Cauchy-Verteilung hat die Besonderheit, dass sie vom Gaußschen Verteilungstyp ist, jedoch hat sie den höchsten Peak und die Schwänze zerfallen sehr langsam. Obwohl MCM Alchimia in geeigneter Weise die Pseudo-Zufalls-Abtastwerte für diese Verteilung erzeugt, wird der Ergebnisgraph wie ein isolierter Peak aussehen, da die Abszissenachse im 99% igen Wahrscheinlichkeitsintervall der Abdeckung liegt. Da der Zerfall der Schwänze so graduell ist, wird der Bereich signifikanter Wahrscheinlichkeiten sehr eng.
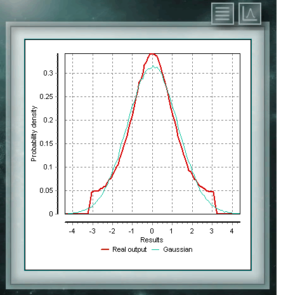Die Verteilung von Von Mises ist eine kontinuierliche Funktion der zirkularen Aufrufe, dh sie sind für die realen im Intervall von 0 bis 2p definiert. Diese Funktion wird derzeit vorzugsweise auf dem Gebiet der Epidemiologie verwendet, um die Ausbreitung von Krankheiten oder technologischen Anwendungen wie der Signalverarbeitung zu beschreiben. Die Von-Mises-Verteilung wird auch als normaler Kreis bezeichnet, da sie dem Gaußschen ähnelt, jedoch auf die Kreisebene beschränkt ist.