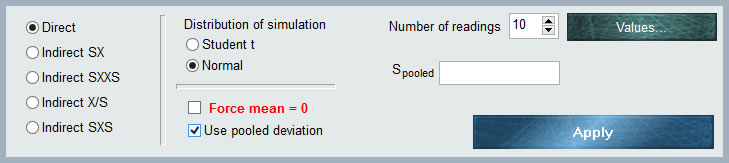
Diese Distribution ist keine Distribution an sich, sondern eine leistungsstarke und exklusive Form von MCM Alchimia, um Rohwerte der Wiederholbarkeit in das Modell unseres Versuchs einzugeben, ohne vorherige Operationen in durchführen zu müssen eine Kalkulationstabelle.
Wie aus der Grafik ersichtlich, verfügt das Eingabedatenfeld über mehrere Selektoren, um die Eingabeeigenschaften unserer Unsicherheitskomponente zu definieren.
1. Eingabedatensatz
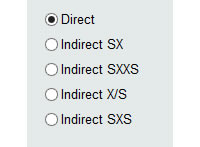 Auf der linken Seite des Bedienfelds befinden sich 5 Auswahlknöpfe (Auswahlschalter), die der Software anzeigen, in welcher Form die Eingabedaten eingegeben werden. Wir haben dann 5 Eingabeformulare:
Auf der linken Seite des Bedienfelds befinden sich 5 Auswahlknöpfe (Auswahlschalter), die der Software anzeigen, in welcher Form die Eingabedaten eingegeben werden. Wir haben dann 5 Eingabeformulare:
- Direkt. Wenn Sie diese Option auswählen, werden wir MCM Alchimia mitteilen, dass wir die Daten einzeln eingeben werden. Aus diesen Daten erhält die Software automatisch den Mittelwert, die Standardabweichung der Stichprobenmittel und die Freiheitsgrade sowie die für die Simulation erforderlichen Statistikparameter.
- Indirekter SX. Diese Option gibt an, dass die Anwendung zwei Datenspalten anfordern soll, von denen jeder Wert für die Wiederholbarkeit aus der Subtraktion Value = (X – S) abgerufen wird. Diese Option kann beispielsweise verwendet werden, wenn zwei digitale Instrumente durch Vergleich kalibriert werden und Sie die Wiederholbarkeit der Fehler berechnen möchten. Wir geben die Ablesung des Musters in der Spalte von S und die Ablesung der Probe in X an. Sie kann auch verwendet werden, wenn das Gewicht einer in einem Tiegel enthaltenen Substanz durch das Gewicht des leeren Tiegels und erhalten werden soll mit dem Inhalt. In diesem Fall können die Massenwerte des leeren Tiegels in S und die Masse des Tiegels mit dem Inhalt in X angegeben werden.
- Indirektes SXXS. In bestimmten Fällen werden die Fehlerwerte aus einer Reihe von Kennzahlen erhalten, die auch als ABBA-Format bezeichnet wird und in einer Tabelle mit 4 Spalten angefordert wird. Dieses Format wird manchmal verwendet, wenn die durch die potentielle Drift der Messinstrumente verursachte Vorspannung beseitigt werden soll. Auf diese Weise erhält man jeden Wert aus der Berechnung Wert = (X1 + X2) / 2 – (S1 + S2) / 2 .
- Indirektes X / S In diesem indirekten Format wird jeder Wert für Wiederholungen aus der Beziehung Value = X / S abgerufen. durch eine Tabelle mit zwei Spalten angegeben.
- Indirektes SXS. Dieses Format ähnelt SXXS, nur in drei Spalten. Die Werte werden automatisch von der Anwendung durch die Operation erhalten: Wert = X – (S1 + S2) / 2 .
2. Einnahme von Werten.
 In der oberen rechten Ecke des MCM-Bedienfelds hat Alchimia ein Feld, in dem die Anzahl der Wiederholungen angegeben werden muss, bis zu der die Simulationsparameter geschätzt werden sollen, d. h. der Mittelwert und die Standardabweichung Strümpfe Standardmäßig hat die Anwendung 10 Werte. Dieser Wert kann jedoch durch manuelles Bearbeiten der Nummer oder mit den Inkrement- / Dekrementpfeilen geändert werden.
In der oberen rechten Ecke des MCM-Bedienfelds hat Alchimia ein Feld, in dem die Anzahl der Wiederholungen angegeben werden muss, bis zu der die Simulationsparameter geschätzt werden sollen, d. h. der Mittelwert und die Standardabweichung Strümpfe Standardmäßig hat die Anwendung 10 Werte. Dieser Wert kann jedoch durch manuelles Bearbeiten der Nummer oder mit den Inkrement- / Dekrementpfeilen geändert werden.
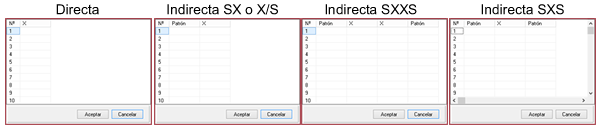
Nachdem wir die Anzahl der Messungen angegeben haben, die eingegeben werden, klicken wir auf die Schaltfläche „Werte“, wo sich ein Raster für die Eingabe von Werten öffnet. Je nach dem im Auswahlfeld für Optionsfelder ausgewählten Einkommensformat enthält die Tabelle die erforderliche Anzahl von Spalten:
3.- Simulationsverteilung.
 In diesem Abschnitt des Fensters können Sie die Simulation anhand der Parameter der zuvor definierten Verteilung anhand der eingegebenen Werte durchführen:
In diesem Abschnitt des Fensters können Sie die Simulation anhand der Parameter der zuvor definierten Verteilung anhand der eingegebenen Werte durchführen:
Studentenverteilung. Bei Auswahl dieser Option berechnet MCM Infinite Alchimia den Mittelwert und die Standardabweichung der Stichprobenmittelwerte aus der eingegebenen Wertetabelle. Dann wird eine randomisierte Verteilung entsprechend der Student-t-Funktion generiert, wobei die Anzahl der Freiheitsgrade der Anzahl der Werte -1 entspricht.
Normal. In diesem Fall führt die Software die gleichen Berechnungen wie zuvor aus und übernimmt dann den inversen Wert der Funktion t (Abdeckungsfaktor k ) für die gewählte Abdeckungswahrscheinlichkeit und die berechneten Freiheitsgrade . Die Simulation wird dann mit einer pseudo-randomisierten Normalverteilung des berechneten Mittelwerts und der Standardabweichung s1 = ks / k ‚ durchgeführt, wobei k‘ der inverse Wert der Verteilung t für die gleiche Wahrscheinlichkeit der Abdeckung, jedoch für unendliche Freiheitsgrade.
Bei einer hohen Anzahl von Freiheitsgraden weisen beide Simulationen ähnliche oder identische Eigenschaften auf. Bei einer Reihe von Freiheitsgraden dagegen <10 Die Ergebnisse beider Simulationen könnten erhebliche Unterschiede aufweisen.
Welches ist dann zu wählen?
Abhängig von dem Nutzen, den wir für diese Anwendung bereitstellen möchten, benötigen wir möglicherweise die eine oder andere Simulationsverteilung, aber für Techniker, die keine Experten für Statistik sind, empfehlen wir die folgende Regel:
- Für die Validierung traditioneller Berechnungsschätzungen gemäß GUM (JCGM 101) werden Routinelabortests, Eignungsprüfungen, GUM vs MCM-Validierung usw. gemäß einer Normalverteilung simuliert.
- Für Forschung, Statistik, Wirtschaft und Fälle, in denen es erforderlich ist, den Einfluss einer Variablen auf die Unsicherheit der Messgröße genau zu kennen, simulieren Sie die Verteilung nach Student t.
4. Forcing Mean = 0.
Diese Option ist vorgesehen, wenn der Steuerpflichtige, für den diese Verteilung gilt, nur aus Unsicherheitsgründen eingegeben werden soll. Auf diese Weise wird der Durchschnittswert der Funktion aufgehoben, so dass der Mittelwert = 0 ist und keinen Wert liefert. Dies ist besonders nützlich, wenn Modellkomponenten vorhanden sind, die mehr als eine Unsicherheit aufweisen, beispielsweise Auflösung und Wiederholgenauigkeit. Auf diese Weise kann es als summierte Variable angegeben werden, eine Konstante mit dem Wert des Parameters und der Rest nur als Unsicherheitsfaktoren mit einem Nullwert. In diesem Fall kann Typ A als experimentell eingestuft werden. Das Beispiel dieser Hilfe verwendet dieses Tool.
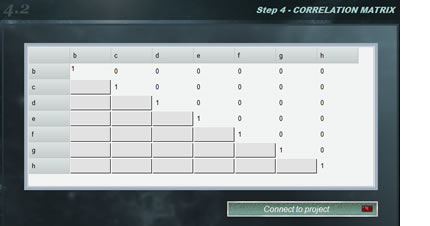 Häufig werden Testmodelle verwendet, die zwei oder mehr Größen mit einem gewissen Korrelationsgrad enthalten, d. h. systematisch, wenn der Wert einer der beiden geändert wird, nimmt die andere zu oder ab. Die Korrelationskoeffizienten zwischen zwei Variablen variieren zwischen -1 und 1, wobei der Wert die Stärke der Korrelation angibt, während das Vorzeichen die Richtung angibt. Auf diese Weise verstehen wir, dass, wenn die Korrelation = 1 ist, eine absolute direkte Proportionalität zwischen den Beträgen besteht, während bei einem Wert von -1 die Proportionalität umgekehrt ist. Andererseits zeigt ein Nullwert für den Korrelationskoeffizienten an, dass die Variablen unabhängig sind.
Häufig werden Testmodelle verwendet, die zwei oder mehr Größen mit einem gewissen Korrelationsgrad enthalten, d. h. systematisch, wenn der Wert einer der beiden geändert wird, nimmt die andere zu oder ab. Die Korrelationskoeffizienten zwischen zwei Variablen variieren zwischen -1 und 1, wobei der Wert die Stärke der Korrelation angibt, während das Vorzeichen die Richtung angibt. Auf diese Weise verstehen wir, dass, wenn die Korrelation = 1 ist, eine absolute direkte Proportionalität zwischen den Beträgen besteht, während bei einem Wert von -1 die Proportionalität umgekehrt ist. Andererseits zeigt ein Nullwert für den Korrelationskoeffizienten an, dass die Variablen unabhängig sind.

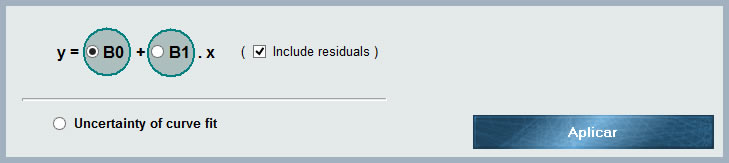

 Auf der linken Seite des Bedienfelds befinden sich 5 Auswahlknöpfe (Auswahlschalter), die der Software anzeigen, in welcher Form die Eingabedaten eingegeben werden. Wir haben dann 5 Eingabeformulare:
Auf der linken Seite des Bedienfelds befinden sich 5 Auswahlknöpfe (Auswahlschalter), die der Software anzeigen, in welcher Form die Eingabedaten eingegeben werden. Wir haben dann 5 Eingabeformulare:
 In diesem Abschnitt des Fensters können Sie die Simulation anhand der Parameter der zuvor definierten Verteilung anhand der eingegebenen Werte durchführen:
In diesem Abschnitt des Fensters können Sie die Simulation anhand der Parameter der zuvor definierten Verteilung anhand der eingegebenen Werte durchführen: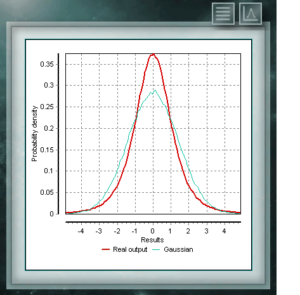 Es ist üblich, bei allen Arten von Analysen, Tests oder Kalibrierungen davon auszugehen, dass sich wiederholende Ereignisse ohne externe Stimuli, die ihre Wahrscheinlichkeiten variieren, gemäß einer durch den Mittelwert definierten Normal- oder Gaußverteilung verteilt werden und die für die Probe berechnete Standardabweichung. Genau genommen trifft dies nur zu, wenn die Anzahl der Wiederholungen groß ist, was mit dem zentralen Grenzwertsatz übereinstimmt. Wenn wir jedoch nicht über ausreichende Informationen verfügen, um die Eigenschaften dieser Gaußschen Verteilung zu beschreiben, weil unsere Untersuchungsstichprobe nicht groß genug ist, nehmen Sie diese Bedingungen an erfüllt sind, werden wir die für unsere Messung unterschätzten Unsicherheitswerte, wie im Leitfaden JCGM 100 – Leitfaden zum Ausdruck der Unsicherheit bei der Messung angegeben, sicherlich überschreiten.
Es ist üblich, bei allen Arten von Analysen, Tests oder Kalibrierungen davon auszugehen, dass sich wiederholende Ereignisse ohne externe Stimuli, die ihre Wahrscheinlichkeiten variieren, gemäß einer durch den Mittelwert definierten Normal- oder Gaußverteilung verteilt werden und die für die Probe berechnete Standardabweichung. Genau genommen trifft dies nur zu, wenn die Anzahl der Wiederholungen groß ist, was mit dem zentralen Grenzwertsatz übereinstimmt. Wenn wir jedoch nicht über ausreichende Informationen verfügen, um die Eigenschaften dieser Gaußschen Verteilung zu beschreiben, weil unsere Untersuchungsstichprobe nicht groß genug ist, nehmen Sie diese Bedingungen an erfüllt sind, werden wir die für unsere Messung unterschätzten Unsicherheitswerte, wie im Leitfaden JCGM 100 – Leitfaden zum Ausdruck der Unsicherheit bei der Messung angegeben, sicherlich überschreiten.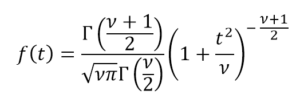
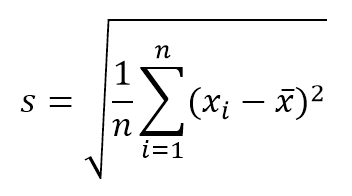
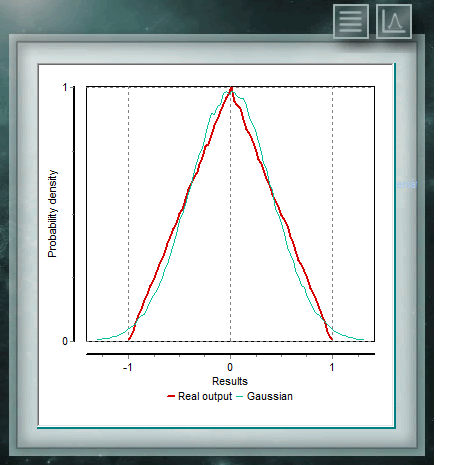 Die durchgehende Dreiecksverteilung ist dadurch gekennzeichnet, dass sie wie im Fall des Rechtecks an zwei Extreme begrenzt ist, aber auch einen Modus (oder einen wahrscheinlicheren Wert) innerhalb dieses Bereichs aufweist. Die Wahrscheinlichkeit in jedem Teilintervall gleicher Länge steigt linear bis zur Art und Weise und fällt dann auf die gleiche Weise bis zur oberen Grenze ab. Diese Verteilung wird häufig in Variablen verwendet, bei denen die Informationen begrenzt sind, wie im Fall der Uniform, bei denen jedoch eine ungefähre Kenntnis des Modalwerts vorliegt, d. H. Wo der genaue Punkt dieses Wertes nicht bekannt ist, jedoch Informationen vorhanden sind der Region oder des Teilintervalls, wo sie zu finden sind.
Die durchgehende Dreiecksverteilung ist dadurch gekennzeichnet, dass sie wie im Fall des Rechtecks an zwei Extreme begrenzt ist, aber auch einen Modus (oder einen wahrscheinlicheren Wert) innerhalb dieses Bereichs aufweist. Die Wahrscheinlichkeit in jedem Teilintervall gleicher Länge steigt linear bis zur Art und Weise und fällt dann auf die gleiche Weise bis zur oberen Grenze ab. Diese Verteilung wird häufig in Variablen verwendet, bei denen die Informationen begrenzt sind, wie im Fall der Uniform, bei denen jedoch eine ungefähre Kenntnis des Modalwerts vorliegt, d. H. Wo der genaue Punkt dieses Wertes nicht bekannt ist, jedoch Informationen vorhanden sind der Region oder des Teilintervalls, wo sie zu finden sind.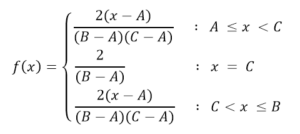
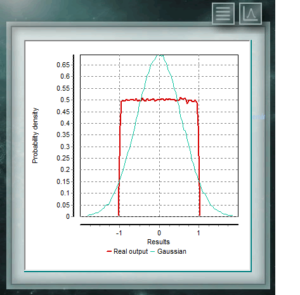 Diese kontinuierliche Verteilung ist dadurch gekennzeichnet, dass sie für jeden Wert des Intervalls die gleiche Wahrscheinlichkeit hat. Es wird häufig für Beiträge von Typ-B-Unsicherheiten verwendet, bei denen nur die Haupt- und Nebenabmessungen des Intervalls bekannt sind, beispielsweise in der Aufteilung oder Auflösung eines digitalen Instruments. In vielen Fällen kann diese Verteilung auch zugeordnet werden, wenn wenig Informationen über die Zufallsvariable, in bibliographischen Daten vorhanden sind oder wenn der Überdeckungsfaktor einer Unsicherheit nicht bekannt ist.
Diese kontinuierliche Verteilung ist dadurch gekennzeichnet, dass sie für jeden Wert des Intervalls die gleiche Wahrscheinlichkeit hat. Es wird häufig für Beiträge von Typ-B-Unsicherheiten verwendet, bei denen nur die Haupt- und Nebenabmessungen des Intervalls bekannt sind, beispielsweise in der Aufteilung oder Auflösung eines digitalen Instruments. In vielen Fällen kann diese Verteilung auch zugeordnet werden, wenn wenig Informationen über die Zufallsvariable, in bibliographischen Daten vorhanden sind oder wenn der Überdeckungsfaktor einer Unsicherheit nicht bekannt ist.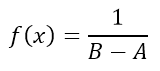
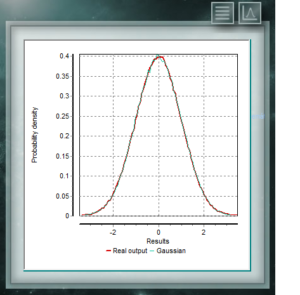 Diese Verteilung ist diejenige, die am häufigsten natürliche und soziale Ereignisse darstellt. Die meisten Beweise aus der klassischen Statistik sowie die Abschätzung von Unsicherheiten beruhen auf der Annahme, dass die Daten einer Normalverteilung entsprechen. Aus theoretischer Sicht behauptet der zentrale Grenzwertsatz, dass bei einer ausreichend großen Stichprobe die Verteilung der Mittel einer annähernd Normalverteilung folgt. Die allgemeine Formel dieser Verteilung lautet:
Diese Verteilung ist diejenige, die am häufigsten natürliche und soziale Ereignisse darstellt. Die meisten Beweise aus der klassischen Statistik sowie die Abschätzung von Unsicherheiten beruhen auf der Annahme, dass die Daten einer Normalverteilung entsprechen. Aus theoretischer Sicht behauptet der zentrale Grenzwertsatz, dass bei einer ausreichend großen Stichprobe die Verteilung der Mittel einer annähernd Normalverteilung folgt. Die allgemeine Formel dieser Verteilung lautet: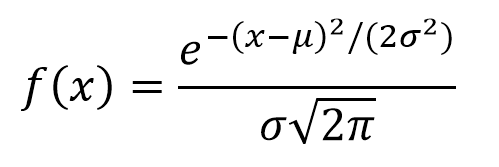
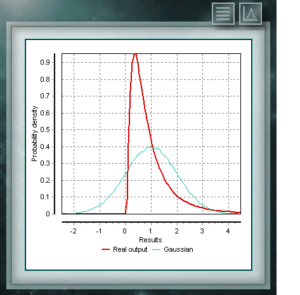 Diese Verteilung stellt Zufallsvariablen dar, deren Logarithmen gemäß einer Normalverteilung verteilt sind. Die logarithmische Normalverteilung nimmt abhängig vom Wert ihres Skalenparameters unterschiedliche Formen an und wird häufig in der Zuverlässigkeit von Hochtechnologieprodukten und auch in mikrobiologischen Zählungen verwendet, da sie auf dem multiplikativen Wachstumsmodell basieren.
Diese Verteilung stellt Zufallsvariablen dar, deren Logarithmen gemäß einer Normalverteilung verteilt sind. Die logarithmische Normalverteilung nimmt abhängig vom Wert ihres Skalenparameters unterschiedliche Formen an und wird häufig in der Zuverlässigkeit von Hochtechnologieprodukten und auch in mikrobiologischen Zählungen verwendet, da sie auf dem multiplikativen Wachstumsmodell basieren.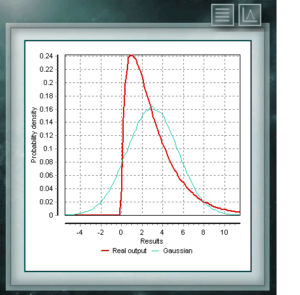 Diese kontinuierliche Wahrscheinlichkeitsverteilung im Bereich der positiven Realen steht in engem Zusammenhang mit der Normalverteilung, zum Beispiel ist sie die Stichprobenverteilung von σ². Die Chi Ssquare-Verteilung wird mit einem einzigen Parameter definiert, bei dem es sich um Freiheitsgrade handelt. Die Funktion ist immer asymmetrisch und nach rechts geneigt. Diese Verteilung wird in verschiedenen Bereichen der Wissenschaft sehr häufig verwendet, da sie die Analyse von Datensätzen ermöglicht und bestimmt, ob der Unterschied zwischen ihnen durch Zufall (Nullhypothese) oder durch einen anderen externen Faktor bedingt ist.
Diese kontinuierliche Wahrscheinlichkeitsverteilung im Bereich der positiven Realen steht in engem Zusammenhang mit der Normalverteilung, zum Beispiel ist sie die Stichprobenverteilung von σ². Die Chi Ssquare-Verteilung wird mit einem einzigen Parameter definiert, bei dem es sich um Freiheitsgrade handelt. Die Funktion ist immer asymmetrisch und nach rechts geneigt. Diese Verteilung wird in verschiedenen Bereichen der Wissenschaft sehr häufig verwendet, da sie die Analyse von Datensätzen ermöglicht und bestimmt, ob der Unterschied zwischen ihnen durch Zufall (Nullhypothese) oder durch einen anderen externen Faktor bedingt ist.