[happyforms id=»8949″ /]

Para abrir el teclado de funciones, hacer click en el enlace f(x) que se encuentra sobre el editor de ecuaciones cuando nos posicionamos en él.

En la sección inferior del teclado de funciones, hay dos botones de interpolacion que permiten obtener resultados de interpolación lineal en la curva conectada. Estas variables genéricas realizan no solo la interpolación en la curva sino que también realizan la estimación de incertidumbre de la misma, integrando su contribución al modelo.

Es importante entender que este cálculo no representa lo que habitualmente se realiza cuando lo hacemos manualmente, sino que integra todas las herramientas disponibles en la simulación del modelo, así como los datos obtenidos durante la simulación de la curva conectada.

REG_y(x). Interpola sobre la respuesta observada (y) de un valor indicado de x, estimando su incertidumbre total asociada. El valor de x puede ser numérico, una variable o incluso parte de la ecuación del modelo. Por ejemplo REG_y(5), REG_y(A) o REG_y(coef_a*ABS(A1-Amedia)).

REG_x(y). Dado un valor, variable o fragmento de ecuación de y, interpola y estima la incertidumbre asociada del correspondiente valor de x.

Incertidumbre de la interpolación.

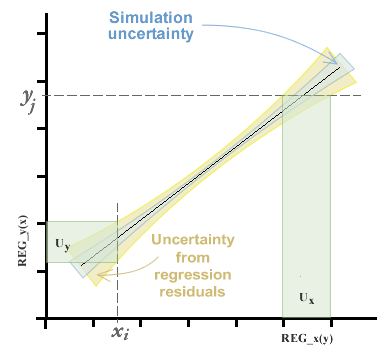
En el capítulo de Uso del panel de curvas de calibración vimos que podíamos estimar la curva de mejor ajuste por el método de mínimos cuadrados ordinarios, inversos y totales (este último por medio del método de análisis del componente primario). Cualquiera sea el método elegido, vamos a obtener coeficientes de la ecuación de la recta, además de un intervalo de incertidumbre variable a lo largo de la curva, compuesto por la incertidumbre de simulación y la aportada por la varianza de los residuos. Este tema puede verse con más profundidad en el capítulo de regresiones y curvas.

La incertidumbre en la interpolación, entonces, estará dada por el error estandar de la curva en el eje del que se pretende interpolar.

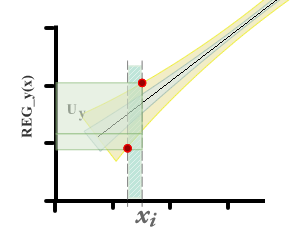
Puede verse que hay dos diferencias respecto al método que suele utilizarse para la estimación de incertidumbre en curvas de calibración. Primeramente, no se espera una incertidumbre nula en el eje x.

Por otra parte, cuando se busca estimar el valor de x_i a partir de un y_i observado, el intervalo de incertidumbre en x es tomado a partir de la varianza de residuos en x. En los gráficos puede verse una representación de la incertidumbre del mesurando en cada caso.

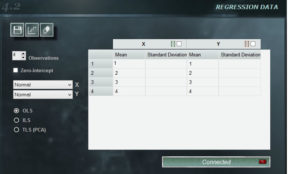El panel de regresiones de MCM Alchimia infinito permite una gran flexibilidad a la hora de construir una curva de calibración para nuestro modelo de ensayo.

Características del Panel

1. Botones de menú. En el sector superior izquierdo del panel hay tres botones que son exclusivos de este panel.

Guardar. Permite guardar los datos digitados para la curva. Estos datos se guardan independientemente del modelo. De esta forma puede utilizarse la misma curva en otros modelos y, a la inversa, utilizar otras curvas de calibración en el mismo modelo cuando sea necesario. Las curvas se guardarán con extensión .mcr.

Abrir curva. Este botón permite abrir una curva de MCM Alchimia previamente guardada. Abrir una curva no implica que quede conectada, por lo que luego de abrirla se debe apretar el botón conectar para que quede conectada.

Limpiar datos. Borra todos los datos digitados en el panel.

2. Numero de observaciones. Utilizando los botones de avance y retroceso puede modificarse el número de observaciones que utilizaremos para definir la curva. El software ofrece 5 por defecto, pero pueden indicarse un número ilimitado de observación con un mínimo de 3.

3. Interceptar con cero. Seleccionando esta opción se obtendrá un término independiente = 0, cualquiera sean los valores de entrada. En determinadas situaciones, puede definirse esta restricción por el conocimiento que se tiene del proceso, para lo cual esta disponible esta opción.

4. Menú de distribuciones. En el extremo superior derecho de este panel están los menúes desplegables donde podemos seleccionar distribuciones de probabilidad, tanto para el termino independiente, como para e dependiente. Las distribuciones disponibles en estos combos son: Constante, Rectangular, Triangular y Normal.

Si se selecciona Constante, se está suponiendo que las entradas en ese eje no tienen incertidumbre por lo que la columna de propiedades quedará inactiva y no se pueden ingresar datos. En los demás casos habra que definir el desvío estándar para el caso de la distribución normal o el semiintervalo para la rectangular o triangular.

5. Panel de datos. En este campo se ingresan los valores medios de x e y, así como las propiedades de la distribución que elegimos para cada eje. Importante !. Este panel permite copiar y pegar datos de cualquier hoja de con la misma forma. Si el rango copiado tiene mayores dimensiones que las indicadas en el panel de datos, los datos sobrantes se truncarán. La celda seleccionada en el panel será la celda superior izquierda del rango copiado.

En la celda de titulo de cada eje existe una casilla de chequeo. Pulsando esta casilla los datos de la primer fila de datos de ese eje se copiarán en todas las filas siguientes.

6. Selector de mínimos cuadrados. En este selector seleccionamos el tipo de método de mínimos cuadrados que se usarán para obtener la curva de calibración.

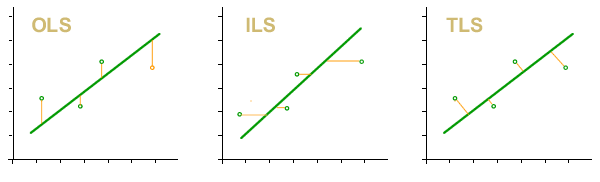
• OLS. Minimos cuadrados ordinarios. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos en y.
• ILS. Minimos cuadrados inversos. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos en x.
• TLS (PCA). Minimos cuadrados totales. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos ortogonales a la curva.

Importante: El presente artículo, y por consiguiente, el uso de la herramienta para curvas de MCM Alchimia no toma en cuenta los supuestos relacionados con la aplicación de mínimos cuadrados ordinarios, normalidad, linealidad, homoscedasticidad, e independencia. El estudio y validación de estos supuestos permiten conocer la calidad y aplicabilidad de la representación lineal a partir de los datos de entrada, sin embargo MCM Alchimia infinito, permite conectar curvas construidas a partir de cualquier juego de datos de entrada realizando mínimos cuadrados no ponerados y no asegura ni controla el cumplimiento de estos supuestos.

Es frecuente encontrar ensayos, métodos analíticos o calibraciones que se basan en la medición a diferentes niveles del analito o en distintas posiciones de la escala de lectura, cuando se trata de un instrumento. De esta forma, en la mayoría de los casos se considera una relación lineal entre ellos, obteniendo por el método de mínimos cuadrados los coeficientes de la ecuación de la recta:

De esta forma cuando se trata de calibración de equipos y se grafica la corrección en función de la escala de lectura, es fácil obtener este valor aplicando la ecuación de arriba, a partir de los coeficientes obtenidos por mínimos cuadrados y la lectura.

Pero también es usual sobre todo en el área de química construír la curva de calibración con materiales de referencia certificados de concentración conocida y luego utilizar esta curva para obtener la concentración de un analito a partir de una respuesta observada.

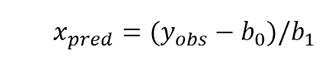
En el análisis de mínimos cuadrados  tenemos tres tipos de incertidumbre asociadas a la curva.

• Errores aleatorios en las respuestas de referencia y_i.
• Efectos aleatorios en los valores de referencia x_i.
• Efecto asociados a la presunción de linealidad, la que estará dada por los residuos.

Si los valores x_i e y_i no presentan incertidumbre, la curva obtenida será aquella que minimiza los cuadrados de los residuos. En caso que los errores aleatorios en valores de referencia x_i y y_i sean mayores que cero, es posible generar pseudoaleatorios con la distribución asociada a cada parámetro, obteniendo por mínimos cuadrados una curva para cada juego de datos. Esto genera una incertidumbre adicional en los coeficientes de regresión, adicional a la incertidumbre determinada por los residuos.

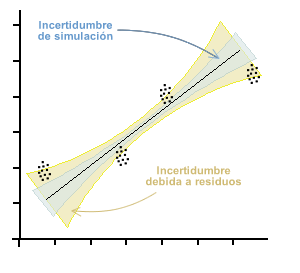
En el gráfico de abajo se presentan simbolicamente el haz de puntos que representaría cada observación si existiera una incertidumbre significativa en ambos ejes. Esta situación por consiguiente arroja un haz de curvas que satifacen los minimos cuadrados de los residuos, generando incertidumbre en ambos coeficientes de regresión. Esta incertidumbre está marcada con celeste en el gráfico.

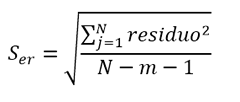
Además esta incertidumbre se verá incrementada por la incertidumbre propia de la curva, la que es determinada en funcion del desvío estandar de los errores residuales. Esta incertidumbre, en general es mayor que la de la simulación y está representado con la zona anaranjada en el gráfico.

¿Que hace MCM Alchimia infinito al conectar una curva?

Luego que se ingresan todos los valores al panel, para poder utilizar la curva en nuestro modelo, debemos «conectar» la curva con el botón dispuesto para ese fin. Cuando hacemos esto, MCM Alchimia infinito realiza una simulacion con el juego de datos, realizando un muestreo aleatorio con los datos de entrada y la respuesta. Para cada una de las iteraciones se obtienen los coeficientes de regresión b₀ y b₁, y un valor del coeficiente de determinación R².

Al igual que en la simulación tradicional, se obtiene una poblacion de datos para estos parámetros con distribución desconocida, ya de dependerá de las distribuciones y valores de los datos de entrada.

Para no hacer suposiciones ni aproximaciones inadecuadas sobre estas propiedades estadísticas, MCM Alchimia infinito guarda el conjunto de valores en vectores asociados a estas variables aleatórias, las cuales estarán disponibles durante todo el proceso.

Por otra parte, con los valores medios de cada par de datos de entrada, la aplicación calcula la incertidumbre de la curva, en función de los residuos de regresión.

Este repositorio de datos del muestreo se utilizarán de acuerdo a la necesidad de nuestro modelo, ya sea para utilizar los coeficientes b₀ y b₁ con su incertidumbre, para considerar la incertidumbre de la curva o para utilizar las funciones de interpolación que se describirán más adelante.

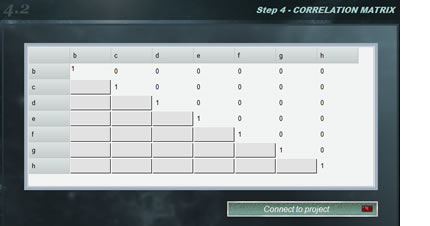Frecuentemente se utilizan modelos de ensayo que contienen dos o más magnitudes con algun grado de correlación, esto es, que sistemáticamente al modificar el valor de una de ellas, la otra aumenta o disminuye. Los coeficientes de correlación entre dos variables varían entre -1 y 1, donde el valor nos indica la fuerza de la correlación, mientras que el signo nos indica la dirección. De este modo, entendemos que si la correlación es = 1 existe una proporcionalidad directa absoluta entre las magnitudes mientras que si el valor es -1 la proporcionalidad es inversa. Por otra parte, un valor cero para el coeficiente de correlación indica que las variables son independientes.

Si conocemos los coeficientes de relación entre las magnitudes del modelo matemático de nuestro ensayo podemos utilizar el panel de correlaciones. La matriz de correlaciones se construye automáticamente con las variables de nuestro modelo para que nosotros indiquemos el coeficiente de correlación entre ellas. Cuando completemos la matriz, pulsamos el botón <conectar al proyecto> y luego de chequear que la matriz sea correcta, la luz verde del botón indicará que está conectada.

En este caso la simulación se hará con variables correlacionadas. Si en algun momento deseamos trabajar con magnitudes independientes nuevamente, solo tenemos que demarcar la casilla de chequeo <correlacionadas> sobre el botón de simulación. De este modo podemos alternar entre ambos estados sin corregir cada vez la matriz de correlaciones.

NOTA: Esta herramienta solo está disponible para modelos con curvas conectadas (Ver trabajo con curvas) 

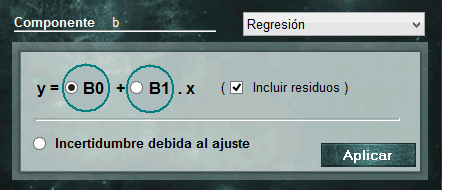Al final de la lista de distribuciones, MCM Alchimia deja disponible a partir de su versión ‘infinito’, esta herramienta que permite asignar parámetros de regresión a nuestro modelo de ensayo. De esta forma, tenemos 3 opciones relacionadas con nuestra curva conectada para escoger:

• B0. Coeficiente independiente (ordenada en el origen) de la curva conectada.
• B1. Coeficiente de primer orden de la curva conectada.

Tanto B0 como B1 tendrán incertidumbres asociadas que corresponden al resultado de la simulación, es decir, si al menos uno de los valores que se utilizaron para construír la curva tenía incertidumbre, la simulación producirá necesariamente una sucesión de curvas para cada juego de valores simulados, cada una con coeficientes B0 y B1 que tendrán algún grado de variación. La magnitud de esta variación esta relacionada con la magnitud de la incertidumbre de los datos de entrada en ambos ejes.

• Incluir residuos. En caso que esta opción esté seleccionada, las incertidumbres asociadas al coeficiente que hayamos seleccionado (B0 o B1) se utilizarán incrementadas en una magnitud determinada por la contribución debida a residuos de mínimos cuadrados. De modo que la incertidumbre asociada a ambos parámetros comprenderan las contribuciones de simulación y de residuos
• Incertidumbre debida al ajuste. Si asignamos esta opción a nuestro parámetro lo que obtendremos es la incertidumbre estandar de la curva conectada debida a residuos, centrada en cero (solo como contribución de incertidumbre). Este valor es el encontrado en regresiones hechas en hoja de cálculo como error típico o error estándar de regresión.

Nota: Es importante hacer notar que si simulamos aisladamente el error típico de una curva, el resultado de desvío estándard de la población resultante es un poco mayor que el mismo parámetro obtenido en una hoja de cálculo. Esto es debido a que si bien la variable se define como de media 0 y desvío = a la incertidumbre típica, la distribución de simulación en MCM Alchimia para este caso no es una Normal, sino una t Student con los grados de libertad que determinan el Nº de puntos con los cuales se construyó la curva, resultando en un desvío mayor para el mesurando.

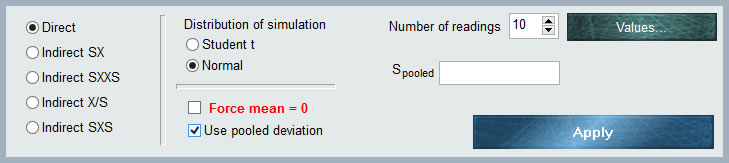Esta distribución no es una distribución en sí misma, sino una potente y exclusiva forma de MCM Alchimia infinito de ingresar valores crudos de repetibilidad al modelo de nuestro ensayo sin necesidad de realizar ningún tipo de dato previo en una hoja de cálculo.

Como puede verse en el gráfico, el panel de datos de entrada tiene varios selectores para definir las características de entrada de nuestro contribuyente de incertidumbre.

1. Juego de datos de entrada

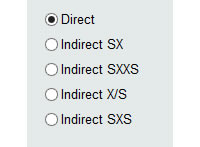A la izquierda del panel tenemos 5 botones de radio (selectores), que indicarán al software la forma que se ingresarán los datos de entrada. Tendremos entonces 5 formas de entrada:

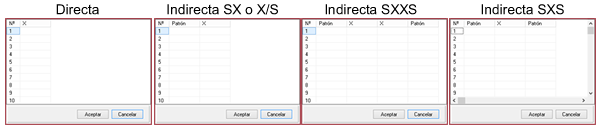
• Directa. Seleccionando esta opción le estaremos diciendo a MCM Alchimia que entraremos los datos uno por uno. De estos datos, el software obtendrá automáticamente la media, desvío estándar de las medias muestrales y grados de libertad, estadísticos necesarios para realizar la simulación.
• Indirecta SX. Esta opción indica que deseamos que la aplicación nos solicite dos columnas de datos, de los cuales cada valor para la repetibilidad se obtendrá de la resta Valor = (X – S). Un ejemplo donde se puede utilizar esta opción es cuando se calibran por comparación dos instrumentos digitales, y se desea calcular la repetibilidad de los errores. Indicamos la lectura del patrón en la columna de S y la lectura de la muestra en X. También puede utilizarse cuando se desea obtener el peso de una sustancia contenida en un crisol,  traves del peso del crisol vacío y con el contenido. En este caso puede indicarse en S los valores de masa del crisol vacío y en X la masa del crisol con el contenido.
• Indirecta SXXS. En determinados casos los valores de error se obtienen a partir de un juego de medidas conocido también como formato como ABBA, el que se solicitará en una tabla de 4 columnas. Este formato es utilizado en ocasiones cuando se desea eliminar el sesgo provocado por la deriva potencial de los instrumentos de medida. De este modo, cada valor será obtenido del cálculo Valor = (X1 + X2) / 2 – (S1 + S2) / 2.
• Indirecta X/S. En este formato indirecto, cada valor para las repeticiones se obtendrá de la relación Valor = X/S, indicada a traves de una tabla de dos columnas.
• Indirecta SXS.  Este formato es similar a SXXS, solo que en tres columnas. Los valores serán obtenidos automáticamente por la aplicación, a traves de la operación: Valor = X – (S1 + S2) / 2.

2. Ingreso de valores.

En el extremo superior derecho del panel MCM Alchimia dispone un campo donde debemos indicar el número de repeticiones al que queremos estimar los parámetros de simulación, esto es, la media y el desvío estándar de las medias. Por defecto la aplicación dispone 10 valores, sin embargo este valor puede cambiarse editando manualmente el número o con las flechas de incremento/decremento.

Luego de indicar el número de mediciones que se ingresarán hacemos click en el botón «Valores», donde se abrirá una grilla para ingreso de valores. Según el formato de ingreso elegido en el selector de juego de valores, la tabla tendrá el número de columnas necesarias:

3.- Distribución de simulación.

Esta sección del panel pone a disposición dos formas de realizar la simulación a partir de los parámetros de la distribución definida anteriormente a partir de los valores ingresados:

t (Student). Seleccionando esta opción, MCM Alchimia infinito calculará la media y el desvío estandar de las medias muestrales a partir de la tabla de valores ingresada. Luego generará aleatorios distribuídos de acuerdo a la función t Student, con un número de grados de libertad igual a la cantidad de valores -1.

Normal. En este caso, el software realizará los mismos cálculos que antes, luego tomará el valor inverso de la función t (factor de covertura k) para la probabilidad de cobertura elegida y los grados de libertad calculados. La simulación entonces se hará con pseudoaleatorios de distribución normal de media calculada y desvio estandar s1= k.s/k’, siendo k’ el valor inverso de la distribución t para la misma probabilidad de cobertura, pero infinitos grados de libertad.

Para un numero alto de grados de libertad ambas simulaciones tendrá características similares o idénticas. En cambio, para un número de grados de libertad < 10 los resultados obtenidos a partir de ambas simulaciones podrían presentar diferencias significativas.

¿Entonces cual elegir?

Según la utilidad que querramos darle a esta aplicación podemos requerir una u otra distribución de simulación, sin embargo para técnicos no expertos en estadística aconsejamos seguir la siguiente regla:

1. Para validación de estimaciones de cálculo tradicional según GUM (JCGM 101), ensayos de rutina de laboratorios, ensayos de aptitud comparacioes, etc. simular de acuerdo a una Normal.
2. Para investigación, estadística, economía y casos donde se requiera conocer en profundidad el impacto de una variable en la incertidumbre del mesurando, simular de acuerdo a una distribución t Student.

4. Forzar media = 0.

Esta opción está prevista cuando queremos que el contribuyente al que se aplique esta distribución solo se ingrese con fines de incertidumbre. De esta forma se anulará el corrimiento de la función para que la media sea = 0 y no aporte valor. Esto es especialmente útil cuando tenemos componentes del modelo que tienen más de una incertidumbre, por ejemplo la resolución y la repetibilidad. De esta forma se puede indicar como variables sumadas, 1 constante con el valor del parámetro y el resto solo como contribuyentes de incertidumbre con media cero. En este caso las Tipo A pueden ponerse como experimentales. El ejemplo de esta ayuda utiliza esta herramienta.

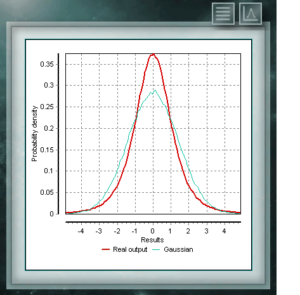Desde hace décadas es usual suponer en todo tipo de análisis, ensayos o calibraciónes que los eventos repetitivos, sin estímulos externos que varíen sus probabilidades, se distribuirán de acuerdo a una distribución Normal o Gaussiana definida por la media y la desvíación estándar calculada en la muestra. En rigor esto solamente es cierto cuando el número de repeticiones es grande, gracias al teorema central del límite, sin embargo cuando no tenemos suficiente información para describir las propiedades de esta Normal debido a que nuestra muestra en estudio no es lo suficientemente grande, suponer que se cumplen igualmente estas condicione, nos arrojará seguramente valores de incertidumbre subestimados para nuestro mesurand .o, gomo lo indica la guía JCGM 100 – Guide to the expression of uncertainty in measurement.

Este mismo problema se lo planteó William Gosset, quien firmaba sus trabajos como Student por razones de confidencialidad empresarial de la compañía donde trabajaba. Gosset necesitaba estimar a partir de datos experimentales, una distribución que representara muestraa pequeñas de varianza desconocida. Esta función distribución propuesta por Gosset se conoce como t Student, y responde a la ecuación general siguiente:

En toda población normalmente distribuída, la distribución t Student permite incrementar el ancho de la distribución normal resultante para incrementar la incertidumbre asociada al mesurando como resultado de la pobreza de información que aporta una muestra pequeña sobre el lote total. En la medida que esta muestra sea mayor, la distribución t se irá acercando a la Normal obtenida a partir del desvio estandar de la muestra hasta ser identica a esta última para infinitas repeticiones del evento.

Lo correcto entonces en todo tipo de análisis es asignar a eventos repetitivos la distribución t con un parámetro gl que serán los grados de libertad, cuyo valor será la cantidad de repeticiones menos 1. MCM Alchimia infinito permite simular la distribución t Student, no solo con este parámetro de forma, sinó con parámetros de escala y de posición, a traves del desvío estandar y la media respectivamente, para que pueda utilizarse en cualquier situación donde corresponda, sin operaciones adicionales.

Parametros de entrada:

• Media. Este parámetro define el desplazamiento de la función en el eje de abscisas. Corresponde al valor medio, o promedio de la variable aleatoria. La colección de datos de esta variable, por tanto, se distribuirán a ambos lados de esta función. En el caso de esta distribución, al igual que en todas las funciones simétricas la media coincidirá con la moda.
• Grados de libertad. Corresponde al número de repeticiones menos 1, Representa el numero de valores que pueden variar sin modificar el valor de la media muestral.
• Desvío estandar. Medida de la dispersión de los valores respecto de la media muestral. Si se utiliza esta distribución para componentes de incertidumbre Tipo A (estadísticos), este valor puede calcularse según la ecuación:
  
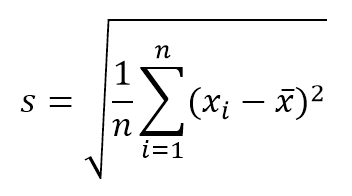
  donde n es el número de valores o repeticiones. Por otra parte, si lo que se desea conocer es el desvío estándar de las medias muestrales, este valor puede obtenerse dividiendo s/√n.

Esta no es una distribución en si misma, sino un valor con incertidumbre cero, como pueden serlo la constante de disociación del agua, la gravedad normal, la temperatura de referencia de un ensayo, la capacidad nominal de un material volumétrico etc. También puede utilizarse para componentes del modelo con varios contribuyentes de incertidumbre, escribiendo el modelo como una constante sumada a una lista de conribuyentes de incertidumbre con valor cero y distribuciones variadas.

Más ayuda

• Distribución Normal (Gaussiana)
• Distribución Rectangular (Uniforme)
• Distribución Triangular
• Constante

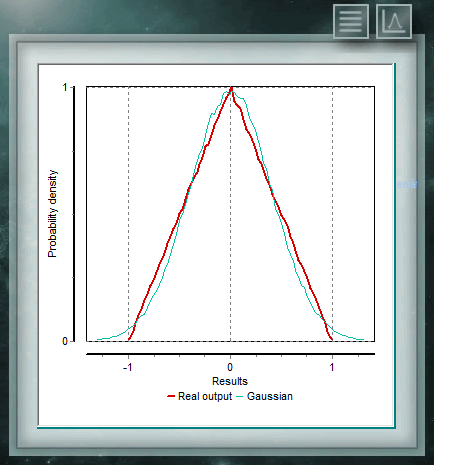La distribución triangular continua se caracteriza por estar acotada a dos extermos como en el caso de la rectangular, pero además tiene una moda (o valor más probabe) dentro de ese intervalo. La probabilidad en cualquier subintervalo de igual longitud irá aumentando linealmente hasta la moda y luego descenderá de la misma forma hasta la cota superior. Esta distribución es muy utilizada en variables donde la información es limitada, como en el caso de la uniforme, pero donde se tiene un conocimiento aproximado del valor Modal, es decir, donde, si bien no se conoce el punto exacto de este valor, se tiene información de la region o subintervalo donde encontrarlo.

Importante: En el caso de MCM Alchimmia, solo está disponible la triangular centrada, esto es, la Moda estadística corresponderá al valor medio del intervalo AB.

La ecuación general entonces, estará definida para el intervalo AB, mientras que fuera de esos extremos la función distribución será 0. La fórmula entonces será:

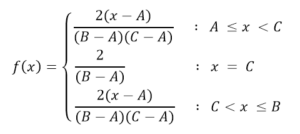
Parametros de entrada:

• Media. Valor medio y valor modal de la variable aleatoria.
• Semi intervalo. Corresponde a la mitad del intervalo al cual se aplica esta distribución, esto es (B-A)/2, siendo A y B, las cotas superior e inferior del intervalo. Cuando esta función es aplicada a la incertidumbre por resolución de un instrumento analógico, este parámetro corresponderá a la apreciación (o estimación <e>). También en el área de química es usual tomar la tolerancia del material volumétrico o incluso de los materiales de referencia como contribuyentes de incertidumbre de distribución tringular (EURACHEM/QUAM:2012 8.1.6). En ambos casos mencionados, el semi intervalo corresponderá al valor e tolerancia del material.

Más ayuda

• Distribución Normal (Gaussiana)
• Distribución Rectangular (Uniforme)
• Distribución Triangular
• Constante