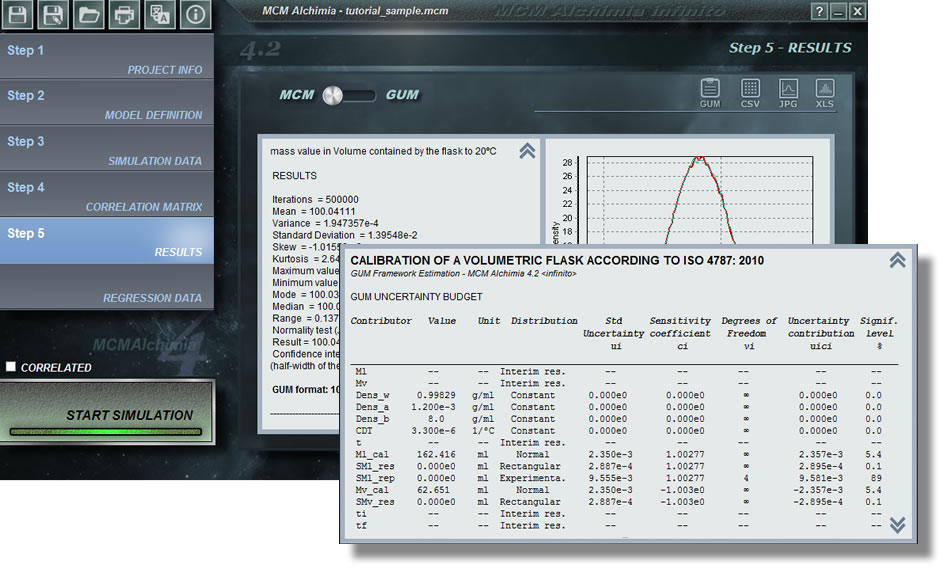
Datos de simulación
Lo único que nos resta por hacer en nuestro primer proyecto es asignar una función distribución de probabilidad a cada variable aleatoria que represente nuestro proyecto. Como se ve en el programa, la grilla está compuesta por varias filas, algunas de ellas están con fondo blanco, y otras conn fondo gris. Las filas que tienen fondo gris corresponden a magnitudes para las cuales no puede asignarse una función distribución, debido a que se trata de resultados o resultados intermedios, esto es, magnitudes que se obtendrán en la simulación como resultado de una ecuación secundaria.
La parte inferior del panel de trabajo presenta un cuadro de comandos que nos ofrecerá una lista desplegable de funciones distribución de probabilidad para que nosotros seleccionemos la que se ajusta a la magnitud de entrada. Luego que hayamos seleccionado una FDP, el cuadro inferior nos pedirá que digitemos los parámetros necesarios para realizar la simulación. Por tanto el proceso de este paso sería como sigue:
- Se recomuenda dejar el número de iteraciones en 500 000 ya que se obtiene in excelente rendimiento en la aplicación y los resultados son absolutamente confiables con este número de iteraciones (puede consultarse el paper: Aspectos computacionales en la estimación de incertidumbres de ensayo por el Método de Monte Carlo)
- Seleccionamos la probabilidad de cobertura para los resultados. Se recomienda utilizar 95.45% con el fin de obtener resultados para K=2.
- Hacemos click en la primer fila con fondo blanco (o llegamos a ella con las teclas de cursor de nuestra computadora)
- Seleccionamos una funcion distribución de probabilidad con la lista desplegable.
- Llenamos los parámetros de simulación en el panel inferior (tener en cuenta las unidades).
- Hacemos click en Aplicar. Si todo es correcto, la fila quedará con fondo verde indicando que la magnitud tiene sus datos de simulación correctamente asignados.
Llendo entonces a nuestro matraz aforado tendremos que:
- V20 : Innhabilitado por ser Resultado, no es posible asignarle una FDP (Función Distribución de Probabilidad)
- Ml : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
- Mv : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
- Dens_w : Asignaremos la PDF Constante de Valor = 0.99829 (g/ml)
- Dens_a : Asignaremos la PDF Constante de Valor = 1,2E-3 (g/ml)
- Dens_b : Asignaremos la PDF Constante de Valor = 8.000 (g/ml)
- CDT : Asignaremos la PDF Constante de Valor = 3.3E-6 (1/ºC)
- t : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
- Ml_cal : Por provenir de una incertidumbre expandida, asignaremos la PDF Normal con el valor promedio de nuestras lecturas, Media = 162,416, ingresando la info del certificado en «Usar certificado», con la incertidumbre = 0,0047 (g) y k = 2
- SM_res : Asignaremos una PDF Rectangular, con Media = 0 (correspondiente a todas las variables que se ingresan solo con fines de estimar incertidumbres) y Semiintervalo = 0,0005, esto es, la mitad de la división de la balanza digital.
- SM_rep : Para la repetibilidad MCM Alchimia infinito, pone a disposición una FDP experimental donde podremos poner directamente los valores medidos y la aplicación se encargará de hacer los cálculos estadísticos necesarios para utilizar esta información por nosotros. Como es solo con fines de incertidumbre habremos de seleccionar «Forzar media = 0». Usaremos la opción «Directa» y haciendo click en el botón Valores ingresaremos las 5 lecturas de nuestro ensayo: 162,384 ; 162,431 ; 162,409 ; 162,417 ; 162,439
- Mv_cal : Por provenir de una incertidumbre expandida, asignaremos la PDF Normal con media en la lectura de la balanza en oportunidad de pesar el matraz vacío, Media = 62,651, ingresando la info del certificado en «Usar certificado», con la incertidumbre = 0,0047 (g) y k = 2
- SMv_res : Asignaremos una PDF Rectangular, con Media = 0 y Semiintervalo = 0,0005.
- ti : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
- tf : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
- corr_t : Asignaremos la PDF Constante de Valor = -0.022 (ºC)
- ti_cal : Por provenir de un certificado de calibración, asignaremos la PDF Normal con el valor de nuestra lectura del termómetro Media = 20,05 . Al mismo tiempo seleccionaremos «Usar certificado» y pondremos la incertidumbre expandida = 0,021 (ºC) y k = 2.
- Sti_res : Para esta medida utilizamos un termómetro de mercurio en vidrio de división: 0,1ºC, del que podemos estimar visualmente 1/4 de la división. De acuerdo a esto, asignaremos una distribución Triangular con Media = 0 y semiintervalo = 0.125 (esto es estimación/2)
- tf_cal : Se da el mismo caso que en ti_cal pero ahora nuestra media será la temperatura final: Media = 20,075, seleccionaremos «Usar certificado» e indicaremos la incertidumbre expandida = 0,021 (ºC) y k = 2.
- Stf_res : igual que Sti_res, esto es, Triangular con Media = 0 y semiintervalo = 0.125.
Al ingresar datos para la última magnitud se iluminará el botón «Iniciar simulación» por lo que ya podremos correr nuestra simulacion y obtener los resultados. Vemos entonces los resultados luego de la simulación.
Más ayuda
 Ésta es una distribución discreta cuyo dominio es el conjunto de los enteros positivos, que representa la cantidad de éxitos que logran en una secuencia de n ensayos. Estos ensayos deben ser de característica dicotómica, esto es, solo ofrecen como resultado dos posibilidades (éxito y fracaso) y tener una probabilidad de éxito definida p.
Ésta es una distribución discreta cuyo dominio es el conjunto de los enteros positivos, que representa la cantidad de éxitos que logran en una secuencia de n ensayos. Estos ensayos deben ser de característica dicotómica, esto es, solo ofrecen como resultado dos posibilidades (éxito y fracaso) y tener una probabilidad de éxito definida p.

 La distribución de Poisson es una distribución discreta definida para el dominio de los números enteros mayores que cero. Se utiliza mayormente para representar la probabilidad de que un número determinado de eventos ocurra en un período de tiempo, una distancia definida, área, volumen, etc.,
La distribución de Poisson es una distribución discreta definida para el dominio de los números enteros mayores que cero. Se utiliza mayormente para representar la probabilidad de que un número determinado de eventos ocurra en un período de tiempo, una distancia definida, área, volumen, etc.,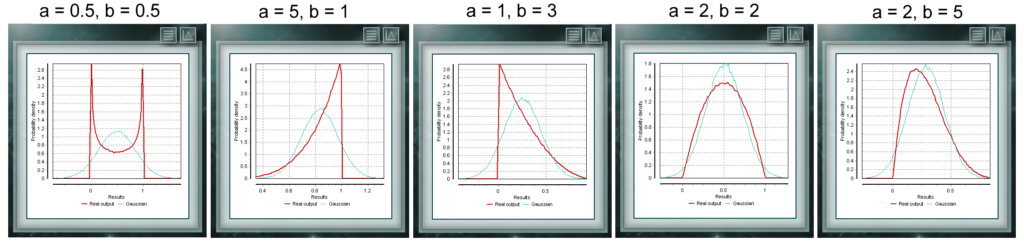 Esta distribución es una función continua con dos parámetros de forma que deben tomar valores reales mayores que cero. La función está definida entre 0 y 1. Un caso particular de la distribución Beta es cuando ambos parámetros de forma toman valores = 1. En este caso la función coincidirá con una distribución uniforme.
Esta distribución es una función continua con dos parámetros de forma que deben tomar valores reales mayores que cero. La función está definida entre 0 y 1. Un caso particular de la distribución Beta es cuando ambos parámetros de forma toman valores = 1. En este caso la función coincidirá con una distribución uniforme.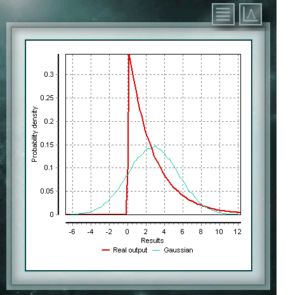 La distribución exponencial de probabilidad es una función continua en el dominio de los reales positivos, que usualmente se utiliza para representar el tiempo entre dos sucesos que se distribuyan según la distribución de poisson, por ejemplo, el tiempo transcurrido hasta que un comercio recibe su primer cliente del día. La distribución exponencial es una caso particular de la distribución Gamma donde el parámetro Forma = 1.
La distribución exponencial de probabilidad es una función continua en el dominio de los reales positivos, que usualmente se utiliza para representar el tiempo entre dos sucesos que se distribuyan según la distribución de poisson, por ejemplo, el tiempo transcurrido hasta que un comercio recibe su primer cliente del día. La distribución exponencial es una caso particular de la distribución Gamma donde el parámetro Forma = 1. Esta distribción es una función continua de carácter sesgado, esto es, donde el valor modal no se corresponde con la media. La distribución Gamma es una generalización de la distribución exponencial, y se usa en general para modelar variables aleatorias que represente el tiempo en que un suceso ocurre un determinado número de veces.
Esta distribción es una función continua de carácter sesgado, esto es, donde el valor modal no se corresponde con la media. La distribución Gamma es una generalización de la distribución exponencial, y se usa en general para modelar variables aleatorias que represente el tiempo en que un suceso ocurre un determinado número de veces.