Esta no es una distribución en si misma, sino un valor con incertidumbre cero, como pueden serlo la constante de disociación del agua, la gravedad normal, la temperatura de referencia de un ensayo, la capacidad nominal de un material volumétrico etc. También puede utilizarse para componentes del modelo con varios contribuyentes de incertidumbre, escribiendo el modelo como una constante sumada a una lista de conribuyentes de incertidumbre con valor cero y distribuciones variadas.
Más ayuda
La distribución triangular continua se caracteriza por estar acotada a dos extermos como en el caso de la rectangular, pero además tiene una moda (o valor más probabe) dentro de ese intervalo. La probabilidad en cualquier subintervalo de igual longitud irá aumentando linealmente hasta la moda y luego descenderá de la misma forma hasta la cota superior. Esta distribución es muy utilizada en variables donde la información es limitada, como en el caso de la uniforme, pero donde se tiene un conocimiento aproximado del valor Modal, es decir, donde, si bien no se conoce el punto exacto de este valor, se tiene información de la region o subintervalo donde encontrarlo.
Importante: En el caso de MCM Alchimmia, solo está disponible la triangular centrada, esto es, la Moda estadística corresponderá al valor medio del intervalo AB.
La ecuación general entonces, estará definida para el intervalo AB, mientras que fuera de esos extremos la función distribución será 0. La fórmula entonces será:
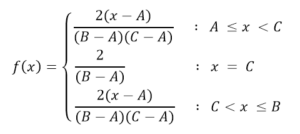
Parametros de entrada:
Más ayuda
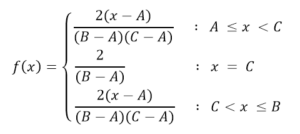
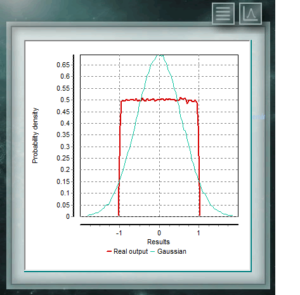Esta distribución continua se caracteriza por se igualmente probable cualquier valor del intervalo. Es ampliamente utilizada para contribuciones de incertidumbres tipo B en las cuales se conocen únicamente las cotas mayor y menor del intervalo, por ejemplo en la división o resolución de un instrumento digital. En muchos caso tambien puede asignarse esta distribución cuando se tiene poca información sobre la variable aleatoria, en datos de bibliografía o cuando no se conoce el factor de cobertura de una incertidumbre,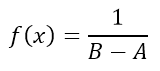
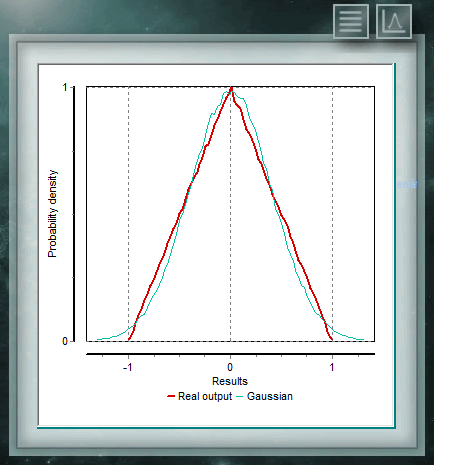
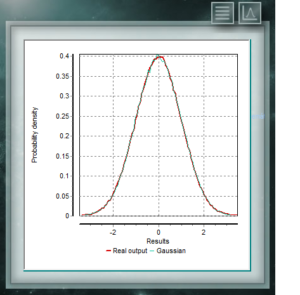La fórmula general de esta distribución está definida para todos los valores de x para los cuales A ≤ x ≤ B, de acuerdo a la ecuación:
Parametros de entrada:
Más Ayuda
Esta distribución es la que más frecuentemennte se encuentra representando eventos naturales y sociales. Gran parte de las pruebas de la estadística clásica, así como de la estimación de incertidumbres se apoyan en la suposición que los datos se ajustan a una distribución normal. Desde la perspectiva teórica, el Teorema del Límite Central sostiene que dada una muestra aleatoria de tamaño suficientemente, grande se observará que la distribución de medias sigue una distribución aproximadamente normal. La fórmula general de esta distribución es: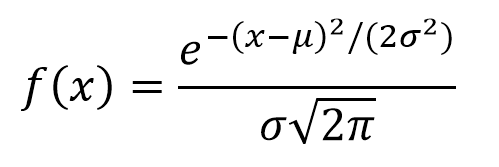
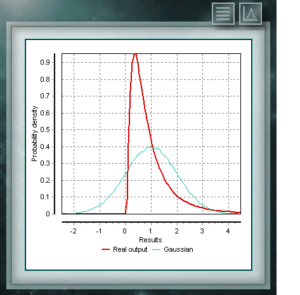donde μ representa la localización y σ la escala de la función. Con el fin de estimar incertidumbres de ensayo, μ corresponde al valor medio y moda de la variable aleatoria, mientras que σ es el desvío estándar.
Parametros de entrada:
Si el parámetro al que se asigna esta distribución corresponde al aporte de incertidumbre proveniente de un certificado de calibración, el desvío estandar corresponde a la incertidumbre estandar (u), o a la incertidumbre expandida dividido el factor de cobertura.
Más ayuda
Esta distribución representa a variables aleatorias cuyos logaritmos estan distribuídos de acuerdo a una distribución normal. La distribución lognormal toma diferentes formas según sea el valor de su parámetro de escala y es de uso frecuente en fiabilidad de productos de alta tecnología y también en conteos microbiológicos ya que se basa en el modelo de crecimiento multiplicativo.
Parámetros de entrada:
Como se indicó, los logaritmos de los valores de la variable aleatoria de distribución lognormal se distribuyen de acuerdo a una función Normal. Esta función distribución puede definirse a partir de dos juegos de parámetros según se seleccione en los botones de radio de la derecha del panel de datos.
Más ayuda
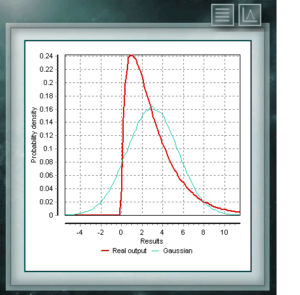Esta distribución de probabilidad continua en el campo de los reales positivos, está íntimamente relacionada con la distribución Normal, por ejemplo, es la distribución muestral de σ². La distribución Xi (o Chi) Cuadrado queda definida con un único parámetro que son los grados de libertad. La función siempre es asimétrica y sesgada a la derecha. Esta distribución se utiliza muy frecuentemente en diversas ramas de la ciencia ya que permite analizar conjuntos de datos y determinar si la diferencia entre ellos es debida al azar (hipótesis nula) o a otro factor externo.
Parámetros de entrada:
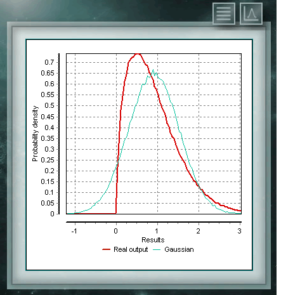Esta distribución es una función continua en el dominio de los números reales positivos, utilizada frecuentemente en economía, meteorología y telecomunicaciones, además de otras aplicaciones específicas, como por ejemplo la tasa de confiabilidad o la sobrevida de organismos o maquinas. Las variables aleatorias que poseen distribución de Weibull modelan la distribución de fallos en sistemas cuando la relacion de fallos se relaciona proporcionalmente a una potencia de tiempo. Esta distribución queda definida a partir de un parámetro de Forma (> 0) característico que indicaría la tasa de fallos, de modo que si la tasa de fallos decrece, es constante o aumenta con el tiempo ya sea si el parámetro k es menor, igual o mayor que 1.
Parámetros de entrada:
Más ayuda
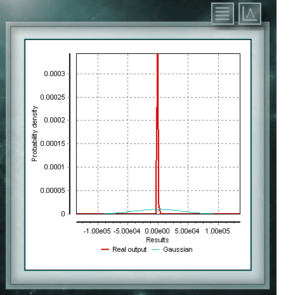La distribución de Cauchy tiene la particularidad de ser del tipo de distribuciones de forma gaussiana, sin embargo tiene el pico más alto y las colas se descomponen muy lentamente. Si bien MCM Alchimia genera adecuadamente los pseudoaleatorios para esta distribución, el gráfico de resultados se verá como un pico aislado ya que el eje de abscisas del mismo se toma en el intervalo de 99% de probabilidad de cobertura. Al ser tan gradual la descomposición de las colas se hace muy estrecho en apariencia el intervalo de probabilidades significativas.
Parámetros de entrada:
Más ayuda
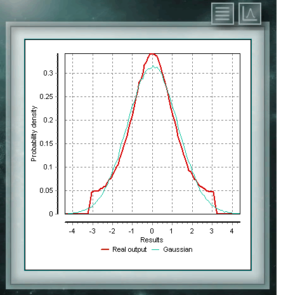La distribución de Von Mises es una función continua de las llamadas circulares, es decir, que están definidas para los reales en el intervalo de 0 a 2π. Esta función es actualmente usada preferentemente en el campo de la epidemiología para describir la propagación de enfermedades o en aplicación tecnológicas como el procesamiento de señales. La distribución Von Mises también es conocida como circular normal ya que es similar a la gaussiana, pero restringida al plano circular.
Parámetros de entrada:
Más ayuda
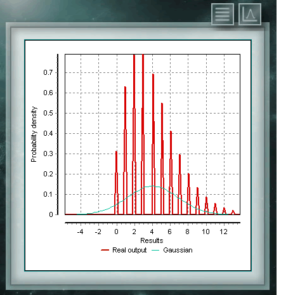La distribución NegBinomial es también una distribución discreta, definida en el dominio de los enteros positivos. Es similar a la binomial excepto que el parámetro n refiere a eventos inexitosos y no totales. Dicho de otra forma, una variable aleatoria con distribución NegBinomial, de parámetros n y p representa la cantidad de éxitos cuya probabilidad es p, que se logran en una secuencia de n ensayos fallidos. Los parámetros por medio de los cuales se define esta distribuición tienen la misma forma que los que representan la distribución Binomial, aunque, como dijimos el parámetro n representa una cualidad diferente.
Parámetros de entrada:
Más ayuda
