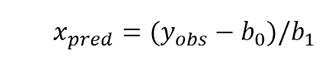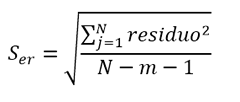Para abrir el teclado de funciones, hacer click en el enlace f(x) que se encuentra sobre el editor de ecuaciones cuando nos posicionamos en él.

En la sección inferior del teclado de funciones, hay dos botones de interpolacion que permiten obtener resultados de interpolación lineal en la curva conectada. Estas variables genéricas realizan no solo la interpolación en la curva sino que también realizan la estimación de incertidumbre de la misma, integrando su contribución al modelo.

Es importante entender que este cálculo no representa lo que habitualmente se realiza cuando lo hacemos manualmente, sino que integra todas las herramientas disponibles en la simulación del modelo, así como los datos obtenidos durante la simulación de la curva conectada.

REG_y(x). Interpola sobre la respuesta observada (y) de un valor indicado de x, estimando su incertidumbre total asociada. El valor de x puede ser numérico, una variable o incluso parte de la ecuación del modelo. Por ejemplo REG_y(5), REG_y(A) o REG_y(coef_a*ABS(A1-Amedia)).

REG_x(y). Dado un valor, variable o fragmento de ecuación de y, interpola y estima la incertidumbre asociada del correspondiente valor de x.

Incertidumbre de la interpolación.

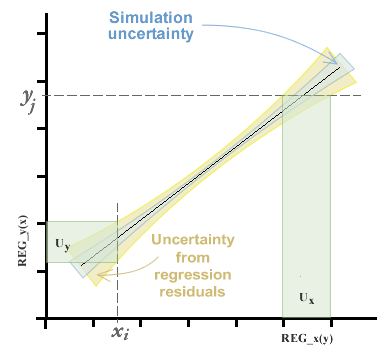
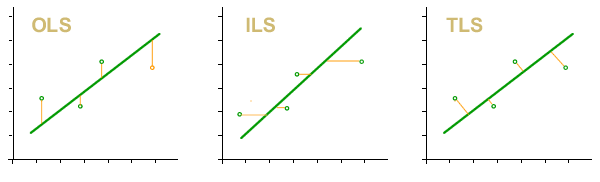
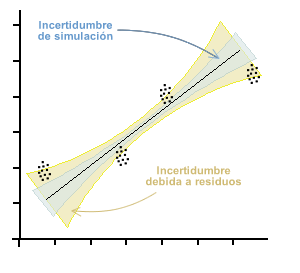
En el capítulo de Uso del panel de curvas de calibración vimos que podíamos estimar la curva de mejor ajuste por el método de mínimos cuadrados ordinarios, inversos y totales (este último por medio del método de análisis del componente primario). Cualquiera sea el método elegido, vamos a obtener coeficientes de la ecuación de la recta, además de un intervalo de incertidumbre variable a lo largo de la curva, compuesto por la incertidumbre de simulación y la aportada por la varianza de los residuos. Este tema puede verse con más profundidad en el capítulo de regresiones y curvas.

La incertidumbre en la interpolación, entonces, estará dada por el error estandar de la curva en el eje del que se pretende interpolar.

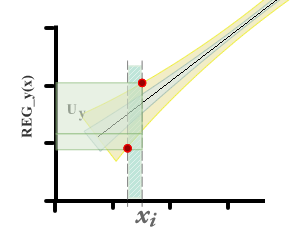
Puede verse que hay dos diferencias respecto al método que suele utilizarse para la estimación de incertidumbre en curvas de calibración. Primeramente, no se espera una incertidumbre nula en el eje x.

Por otra parte, cuando se busca estimar el valor de x_i a partir de un y_i observado, el intervalo de incertidumbre en x es tomado a partir de la varianza de residuos en x. En los gráficos puede verse una representación de la incertidumbre del mesurando en cada caso.

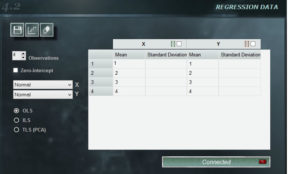El panel de regresiones de MCM Alchimia infinito permite una gran flexibilidad a la hora de construir una curva de calibración para nuestro modelo de ensayo.

Características del Panel

1. Botones de menú. En el sector superior izquierdo del panel hay tres botones que son exclusivos de este panel.

Guardar. Permite guardar los datos digitados para la curva. Estos datos se guardan independientemente del modelo. De esta forma puede utilizarse la misma curva en otros modelos y, a la inversa, utilizar otras curvas de calibración en el mismo modelo cuando sea necesario. Las curvas se guardarán con extensión .mcr.

Abrir curva. Este botón permite abrir una curva de MCM Alchimia previamente guardada. Abrir una curva no implica que quede conectada, por lo que luego de abrirla se debe apretar el botón conectar para que quede conectada.

Limpiar datos. Borra todos los datos digitados en el panel.

2. Numero de observaciones. Utilizando los botones de avance y retroceso puede modificarse el número de observaciones que utilizaremos para definir la curva. El software ofrece 5 por defecto, pero pueden indicarse un número ilimitado de observación con un mínimo de 3.

3. Interceptar con cero. Seleccionando esta opción se obtendrá un término independiente = 0, cualquiera sean los valores de entrada. En determinadas situaciones, puede definirse esta restricción por el conocimiento que se tiene del proceso, para lo cual esta disponible esta opción.

4. Menú de distribuciones. En el extremo superior derecho de este panel están los menúes desplegables donde podemos seleccionar distribuciones de probabilidad, tanto para el termino independiente, como para e dependiente. Las distribuciones disponibles en estos combos son: Constante, Rectangular, Triangular y Normal.

Si se selecciona Constante, se está suponiendo que las entradas en ese eje no tienen incertidumbre por lo que la columna de propiedades quedará inactiva y no se pueden ingresar datos. En los demás casos habra que definir el desvío estándar para el caso de la distribución normal o el semiintervalo para la rectangular o triangular.

5. Panel de datos. En este campo se ingresan los valores medios de x e y, así como las propiedades de la distribución que elegimos para cada eje. Importante !. Este panel permite copiar y pegar datos de cualquier hoja de con la misma forma. Si el rango copiado tiene mayores dimensiones que las indicadas en el panel de datos, los datos sobrantes se truncarán. La celda seleccionada en el panel será la celda superior izquierda del rango copiado.

En la celda de titulo de cada eje existe una casilla de chequeo. Pulsando esta casilla los datos de la primer fila de datos de ese eje se copiarán en todas las filas siguientes.

6. Selector de mínimos cuadrados. En este selector seleccionamos el tipo de método de mínimos cuadrados que se usarán para obtener la curva de calibración.

• OLS. Minimos cuadrados ordinarios. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos en y.
• ILS. Minimos cuadrados inversos. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos en x.
• TLS (PCA). Minimos cuadrados totales. La curva obtenida a traves de este método será aquella para la cual es mínima la suma cuadratica de los residuos ortogonales a la curva.

Importante: El presente artículo, y por consiguiente, el uso de la herramienta para curvas de MCM Alchimia no toma en cuenta los supuestos relacionados con la aplicación de mínimos cuadrados ordinarios, normalidad, linealidad, homoscedasticidad, e independencia. El estudio y validación de estos supuestos permiten conocer la calidad y aplicabilidad de la representación lineal a partir de los datos de entrada, sin embargo MCM Alchimia infinito, permite conectar curvas construidas a partir de cualquier juego de datos de entrada realizando mínimos cuadrados no ponerados y no asegura ni controla el cumplimiento de estos supuestos.

Es frecuente encontrar ensayos, métodos analíticos o calibraciones que se basan en la medición a diferentes niveles del analito o en distintas posiciones de la escala de lectura, cuando se trata de un instrumento. De esta forma, en la mayoría de los casos se considera una relación lineal entre ellos, obteniendo por el método de mínimos cuadrados los coeficientes de la ecuación de la recta:

De esta forma cuando se trata de calibración de equipos y se grafica la corrección en función de la escala de lectura, es fácil obtener este valor aplicando la ecuación de arriba, a partir de los coeficientes obtenidos por mínimos cuadrados y la lectura.

Pero también es usual sobre todo en el área de química construír la curva de calibración con materiales de referencia certificados de concentración conocida y luego utilizar esta curva para obtener la concentración de un analito a partir de una respuesta observada.

En el análisis de mínimos cuadrados  tenemos tres tipos de incertidumbre asociadas a la curva.

• Errores aleatorios en las respuestas de referencia y_i.
• Efectos aleatorios en los valores de referencia x_i.
• Efecto asociados a la presunción de linealidad, la que estará dada por los residuos.

Si los valores x_i e y_i no presentan incertidumbre, la curva obtenida será aquella que minimiza los cuadrados de los residuos. En caso que los errores aleatorios en valores de referencia x_i y y_i sean mayores que cero, es posible generar pseudoaleatorios con la distribución asociada a cada parámetro, obteniendo por mínimos cuadrados una curva para cada juego de datos. Esto genera una incertidumbre adicional en los coeficientes de regresión, adicional a la incertidumbre determinada por los residuos.

En el gráfico de abajo se presentan simbolicamente el haz de puntos que representaría cada observación si existiera una incertidumbre significativa en ambos ejes. Esta situación por consiguiente arroja un haz de curvas que satifacen los minimos cuadrados de los residuos, generando incertidumbre en ambos coeficientes de regresión. Esta incertidumbre está marcada con celeste en el gráfico.

Además esta incertidumbre se verá incrementada por la incertidumbre propia de la curva, la que es determinada en funcion del desvío estandar de los errores residuales. Esta incertidumbre, en general es mayor que la de la simulación y está representado con la zona anaranjada en el gráfico.

¿Que hace MCM Alchimia infinito al conectar una curva?

Luego que se ingresan todos los valores al panel, para poder utilizar la curva en nuestro modelo, debemos «conectar» la curva con el botón dispuesto para ese fin. Cuando hacemos esto, MCM Alchimia infinito realiza una simulacion con el juego de datos, realizando un muestreo aleatorio con los datos de entrada y la respuesta. Para cada una de las iteraciones se obtienen los coeficientes de regresión b₀ y b₁, y un valor del coeficiente de determinación R².

Al igual que en la simulación tradicional, se obtiene una poblacion de datos para estos parámetros con distribución desconocida, ya de dependerá de las distribuciones y valores de los datos de entrada.

Para no hacer suposiciones ni aproximaciones inadecuadas sobre estas propiedades estadísticas, MCM Alchimia infinito guarda el conjunto de valores en vectores asociados a estas variables aleatórias, las cuales estarán disponibles durante todo el proceso.

Por otra parte, con los valores medios de cada par de datos de entrada, la aplicación calcula la incertidumbre de la curva, en función de los residuos de regresión.

Este repositorio de datos del muestreo se utilizarán de acuerdo a la necesidad de nuestro modelo, ya sea para utilizar los coeficientes b₀ y b₁ con su incertidumbre, para considerar la incertidumbre de la curva o para utilizar las funciones de interpolación que se describirán más adelante.