Weibull.
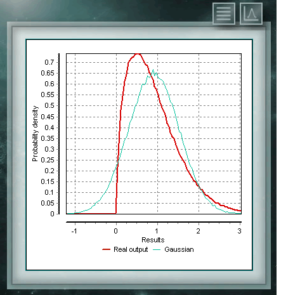Esta distribución es una función continua en el dominio de los números reales positivos, utilizada frecuentemente en economía, meteorología y telecomunicaciones, además de otras aplicaciones específicas, como por ejemplo la tasa de confiabilidad o la sobrevida de organismos o maquinas. Las variables aleatorias que poseen distribución de Weibull modelan la distribución de fallos en sistemas cuando la relacion de fallos se relaciona proporcionalmente a una potencia de tiempo. Esta distribución queda definida a partir de un parámetro de Forma (> 0) característico que indicaría la tasa de fallos, de modo que si la tasa de fallos decrece, es constante o aumenta con el tiempo ya sea si el parámetro k es menor, igual o mayor que 1.
Parámetros de entrada:
- Forma (Shape). Este parámetro define la forma de la distribución. Puede tomar como valor cualquier número del campo de los reales mayores que cero.
- Escala. Este segundo parámetro permite escalar los valores resultantes generando pseudoaleatoreos con la misma forma pero mayor std.
Más ayuda
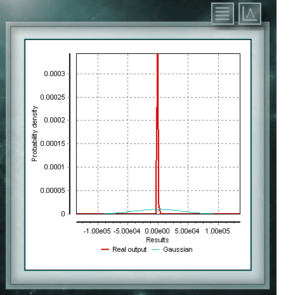La distribución de Cauchy tiene la particularidad de ser del tipo de distribuciones de forma gaussiana, sin embargo tiene el pico más alto y las colas se descomponen muy lentamente. Si bien MCM Alchimia genera adecuadamente los pseudoaleatorios para esta distribución, el gráfico de resultados se verá como un pico aislado ya que el eje de abscisas del mismo se toma en el intervalo de 99% de probabilidad de cobertura. Al ser tan gradual la descomposición de las colas se hace muy estrecho en apariencia el intervalo de probabilidades significativas.
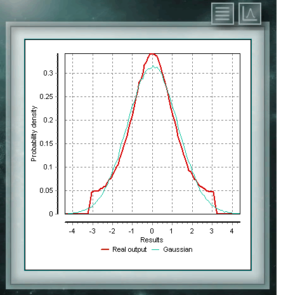La distribución de Von Mises es una función continua de las llamadas circulares, es decir, que están definidas para los reales en el intervalo de 0 a 2π. Esta función es actualmente usada preferentemente en el campo de la epidemiología para describir la propagación de enfermedades o en aplicación tecnológicas como el procesamiento de señales. La distribución Von Mises también es conocida como circular normal ya que es similar a la gaussiana, pero restringida al plano circular.
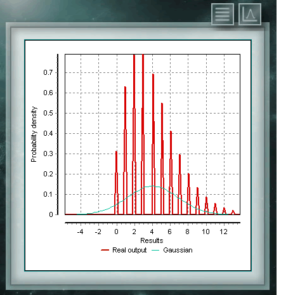La distribución NegBinomial es también una distribución discreta, definida en el dominio de los enteros positivos. Es similar a la binomial excepto que el parámetro n refiere a eventos inexitosos y no totales. Dicho de otra forma, una variable aleatoria con distribución NegBinomial, de parámetros n y p representa la cantidad de éxitos cuya probabilidad es p, que se logran en una secuencia de n ensayos fallidos. Los parámetros por medio de los cuales se define esta distribuición tienen la misma forma que los que representan la distribución Binomial, aunque, como dijimos el parámetro n representa una cualidad diferente.
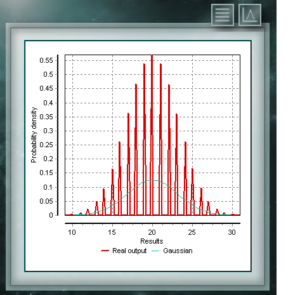Ésta es una distribución discreta cuyo dominio es el conjunto de los enteros positivos, que representa la cantidad de éxitos que logran en una secuencia de n ensayos. Estos ensayos deben ser de característica dicotómica, esto es, solo ofrecen como resultado dos posibilidades (éxito y fracaso) y tener una probabilidad de éxito definida p.
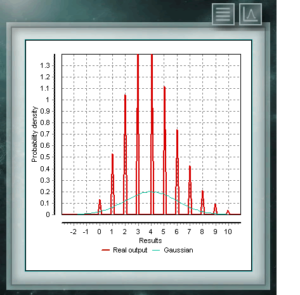La distribución de Poisson es una distribución discreta definida para el dominio de los números enteros mayores que cero. Se utiliza mayormente para representar la probabilidad de que un número determinado de eventos ocurra en un período de tiempo, una distancia definida, área, volumen, etc.,
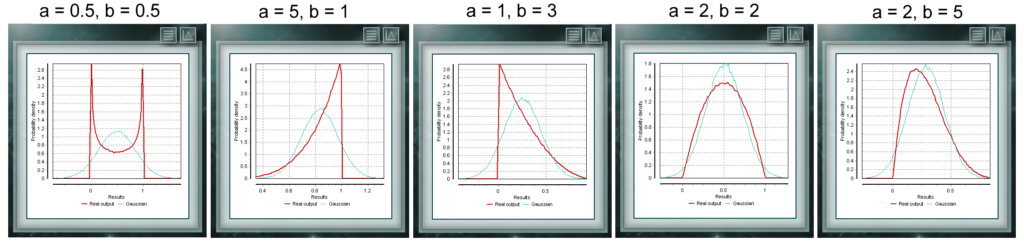Esta distribución es una función continua con dos parámetros de forma que deben tomar valores reales mayores que cero. La función está definida entre 0 y 1. Un caso particular de la distribución Beta es cuando ambos parámetros de forma toman valores = 1. En este caso la función coincidirá con una distribución uniforme.
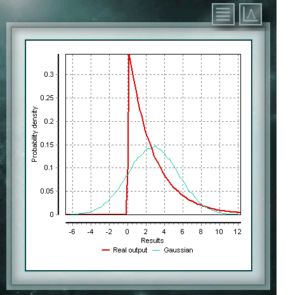La distribución exponencial de probabilidad es una función continua en el dominio de los reales positivos, que usualmente se utiliza para representar el tiempo entre dos sucesos que se distribuyan según la distribución de poisson, por ejemplo, el tiempo transcurrido hasta que un comercio recibe su primer cliente del día. La distribución exponencial es una caso particular de la distribución Gamma donde el parámetro Forma = 1.
Esta distribción es una función continua de carácter sesgado, esto es, donde el valor modal no se corresponde con la media. La distribución Gamma es una generalización de la distribución exponencial, y se usa en general para modelar variables aleatorias que represente el tiempo en que un suceso ocurre un determinado número de veces.