 Esta distribución no es una distribución en sí misma, sino una potente y exclusiva forma de MCM Alchimia infinito de ingresar valores crudos de repetibilidad al modelo de nuestro ensayo sin necesidad de realizar ningún tipo de dato previo en una hoja de cálculo.
Esta distribución no es una distribución en sí misma, sino una potente y exclusiva forma de MCM Alchimia infinito de ingresar valores crudos de repetibilidad al modelo de nuestro ensayo sin necesidad de realizar ningún tipo de dato previo en una hoja de cálculo.
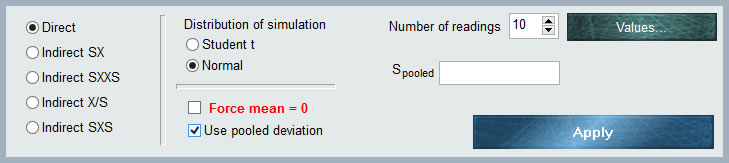
Como puede verse en el gráfico, el panel de datos de entrada tiene varios selectores para definir las características de entrada de nuestro contribuyente de incertidumbre.
- Juego de datos de entrada
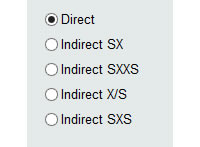 A la izquierda del panel tenemos 5 botones de radio (selectores), que indicarán al software la forma que se ingresarán los datos de entrada. Tendremos entonces 5 formas de entrada:
A la izquierda del panel tenemos 5 botones de radio (selectores), que indicarán al software la forma que se ingresarán los datos de entrada. Tendremos entonces 5 formas de entrada:
- Directa. Seleccionando esta opción le estaremos diciendo a MCM Alchimia que entraremos los datos uno por uno. De estos datos, el software obtendrá automáticamente la media, desvío estándar de las medias muestrales y grados de libertad, estadísticos necesarios para realizar la simulación.
- Indirecta SX. Esta opción indica que deseamos que la aplicación nos solicite dos columnas de datos, de los cuales cada valor para la repetibilidad se obtendrá de la resta Valor = (X – S). Un ejemplo donde se puede utilizar esta opción es cuando se calibran por comparación dos instrumentos digitales, y se desea calcular la repetibilidad de los errores. Indicamos la lectura del patrón en la columna de S y la lectura de la muestra en X. También puede utilizarse cuando se desea obtener el peso de una sustancia contenida en un crisol, traves del peso del crisol vacío y con el contenido. En este caso puede indicarse en S los valores de masa del crisol vacío y en X la masa del crisol con el contenido.
- Indirecta SXXS. En determinados casos los valores de error se obtienen a partir de un juego de medidas conocido también como formato como ABBA, el que se solicitará en una tabla de 4 columnas. Este formato es utilizado en ocasiones cuando se desea eliminar el sesgo provocado por la deriva potencial de los instrumentos de medida. De este modo, cada valor será obtenido del cálculo Valor = (X1 + X2) / 2 – (S1 + S2) / 2.
- Indirecta X/S. En este formato indirecto, cada valor para las repeticiones se obtendrá de la relación Valor = X/S, indicada a traves de una tabla de dos columnas.
- Indirecta SXS. Este formato es similar a SXXS, solo que en tres columnas. Los valores serán obtenidos automáticamente por la aplicación, a traves de la operación: Valor = X – (S1 + S2) / 2.
2. Ingreso de valores.
 En el extremo superior derecho del panel MCM Alchimia dispone un campo donde debemos indicar el número de repeticiones al que queremos estimar los parámetros de simulación, esto es, la media y el desvío estándar de las medias. Por defecto la aplicación dispone 10 valores, sin embargo este valor puede cambiarse editando manualmente el número o con las flechas de incremento/decremento.
En el extremo superior derecho del panel MCM Alchimia dispone un campo donde debemos indicar el número de repeticiones al que queremos estimar los parámetros de simulación, esto es, la media y el desvío estándar de las medias. Por defecto la aplicación dispone 10 valores, sin embargo este valor puede cambiarse editando manualmente el número o con las flechas de incremento/decremento.
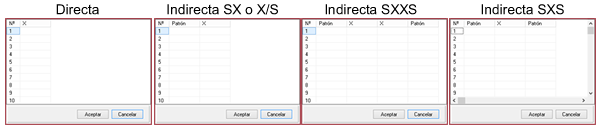
Luego de indicar el número de mediciones que se ingresarán hacemos click en el botón «Valores», donde se abrirá una grilla para ingreso de valores. Según el formato de ingreso elegido en el selector de juego de valores, la tabla tendrá el número de columnas necesarias:
3.- Distribución de simulación.
 Esta sección del panel pone a disposición dos formas de realizar la simulación a partir de los parámetros de la distribución definida anteriormente a partir de los valores ingresados:
Esta sección del panel pone a disposición dos formas de realizar la simulación a partir de los parámetros de la distribución definida anteriormente a partir de los valores ingresados:
t (Student). Seleccionando esta opción, MCM Alchimia infinito calculará la media y el desvío estandar de las medias muestrales a partir de la tabla de valores ingresada. Luego generará aleatorios distribuídos de acuerdo a la función t Student, con un número de grados de libertad igual a la cantidad de valores -1.
Normal. En este caso, el software realizará los mismos cálculos que antes, luego tomará el valor inverso de la función t (factor de covertura k) para la probabilidad de cobertura elegida y los grados de libertad calculados. La simulación entonces se hará con pseudoaleatorios de distribución normal de media calculada y desvio estandar s1= k.s/k’, siendo k’ el valor inverso de la distribución t para la misma probabilidad de cobertura, pero infinitos grados de libertad.
Para un numero alto de grados de libertad ambas simulaciones tendrá características similares o idénticas. En cambio, para un número de grados de libertad < 10 los resultados obtenidos a partir de ambas simulaciones podrían presentar diferencias significativas.
¿Entonces cual elegir?
Según la utilidad que querramos darle a esta aplicación podemos requerir una u otra distribución de simulación, sin embargo para técnicos no expertos en estadística aconsejamos seguir la siguiente regla:
- Para validación de estimaciones de cálculo tradicional según GUM (JCGM 101), ensayos de rutina de laboratorios, ensayos de aptitud comparacioes, etc. simular de acuerdo a una Normal.
- Para investigación, estadística, economía y casos donde se requiera conocer en profundidad el impacto de una variable en la incertidumbre del mesurando, simular de acuerdo a una distribución t Student.
4. Forzar media = 0.
Esta opción está prevista cuando queremos que el contribuyente al que se aplique esta distribución solo se ingrese con fines de incertidumbre. De esta forma se anulará el corrimiento de la función para que la media sea = 0 y no aporte valor. Esto es especialmente útil cuando tenemos componentes del modelo que tienen más de una incertidumbre, por ejemplo la resolución y la repetibilidad. De esta forma se puede indicar como variables sumadas, 1 constante con el valor del parámetro y el resto solo como contribuyentes de incertidumbre con media cero. En este caso las Tipo A pueden ponerse como experimentales. El ejemplo de esta ayuda utiliza esta herramienta.
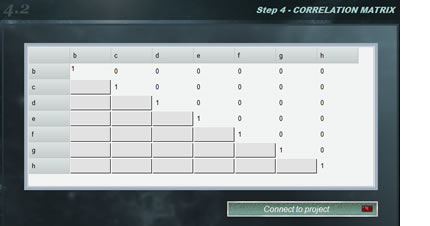 Frecuentemente se utilizan modelos de ensayo que contienen dos o más magnitudes con algun grado de correlación, esto es, que sistemáticamente al modificar el valor de una de ellas, la otra aumenta o disminuye. Los coeficientes de correlación entre dos variables varían entre -1 y 1, donde el valor nos indica la fuerza de la correlación, mientras que el signo nos indica la dirección. De este modo, entendemos que si la correlación es = 1 existe una proporcionalidad directa absoluta entre las magnitudes mientras que si el valor es -1 la proporcionalidad es inversa. Por otra parte, un valor cero para el coeficiente de correlación indica que las variables son independientes.
Frecuentemente se utilizan modelos de ensayo que contienen dos o más magnitudes con algun grado de correlación, esto es, que sistemáticamente al modificar el valor de una de ellas, la otra aumenta o disminuye. Los coeficientes de correlación entre dos variables varían entre -1 y 1, donde el valor nos indica la fuerza de la correlación, mientras que el signo nos indica la dirección. De este modo, entendemos que si la correlación es = 1 existe una proporcionalidad directa absoluta entre las magnitudes mientras que si el valor es -1 la proporcionalidad es inversa. Por otra parte, un valor cero para el coeficiente de correlación indica que las variables son independientes.

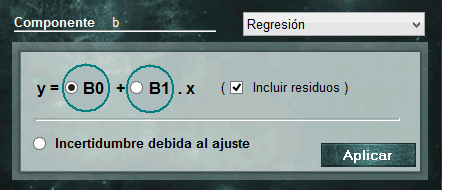 Al final de la lista de distribuciones, MCM Alchimia deja disponible a partir de su versión ‘infinito’, esta herramienta que permite asignar parámetros de regresión a nuestro modelo de ensayo. De esta forma, tenemos 3 opciones relacionadas con nuestra curva conectada para escoger:
Al final de la lista de distribuciones, MCM Alchimia deja disponible a partir de su versión ‘infinito’, esta herramienta que permite asignar parámetros de regresión a nuestro modelo de ensayo. De esta forma, tenemos 3 opciones relacionadas con nuestra curva conectada para escoger: Esta distribución no es una distribución en sí misma, sino una potente y exclusiva forma de MCM Alchimia infinito de ingresar valores crudos de repetibilidad al modelo de nuestro ensayo sin necesidad de realizar ningún tipo de dato previo en una hoja de cálculo.
Esta distribución no es una distribución en sí misma, sino una potente y exclusiva forma de MCM Alchimia infinito de ingresar valores crudos de repetibilidad al modelo de nuestro ensayo sin necesidad de realizar ningún tipo de dato previo en una hoja de cálculo. A la izquierda del panel tenemos 5 botones de radio (selectores), que indicarán al software la forma que se ingresarán los datos de entrada. Tendremos entonces 5 formas de entrada:
A la izquierda del panel tenemos 5 botones de radio (selectores), que indicarán al software la forma que se ingresarán los datos de entrada. Tendremos entonces 5 formas de entrada:
 Esta sección del panel pone a disposición dos formas de realizar la simulación a partir de los parámetros de la distribución definida anteriormente a partir de los valores ingresados:
Esta sección del panel pone a disposición dos formas de realizar la simulación a partir de los parámetros de la distribución definida anteriormente a partir de los valores ingresados: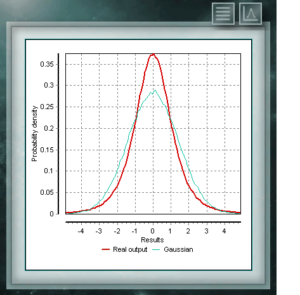 Desde hace décadas es usual suponer en todo tipo de análisis, ensayos o calibraciónes que los eventos repetitivos, sin estímulos externos que varíen sus probabilidades, se distribuirán de acuerdo a una distribución Normal o Gaussiana definida por la media y la desvíación estándar calculada en la muestra. En rigor esto solamente es cierto cuando el número de repeticiones es grande, gracias al teorema central del límite, sin embargo cuando no tenemos suficiente información para describir las propiedades de esta Normal debido a que nuestra muestra en estudio no es lo suficientemente grande, suponer que se cumplen igualmente estas condicione, nos arrojará seguramente valores de incertidumbre subestimados para nuestro mesurand .o, gomo lo indica la guía JCGM 100 – Guide to the expression of uncertainty in measurement.
Desde hace décadas es usual suponer en todo tipo de análisis, ensayos o calibraciónes que los eventos repetitivos, sin estímulos externos que varíen sus probabilidades, se distribuirán de acuerdo a una distribución Normal o Gaussiana definida por la media y la desvíación estándar calculada en la muestra. En rigor esto solamente es cierto cuando el número de repeticiones es grande, gracias al teorema central del límite, sin embargo cuando no tenemos suficiente información para describir las propiedades de esta Normal debido a que nuestra muestra en estudio no es lo suficientemente grande, suponer que se cumplen igualmente estas condicione, nos arrojará seguramente valores de incertidumbre subestimados para nuestro mesurand .o, gomo lo indica la guía JCGM 100 – Guide to the expression of uncertainty in measurement.
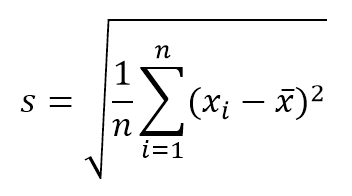
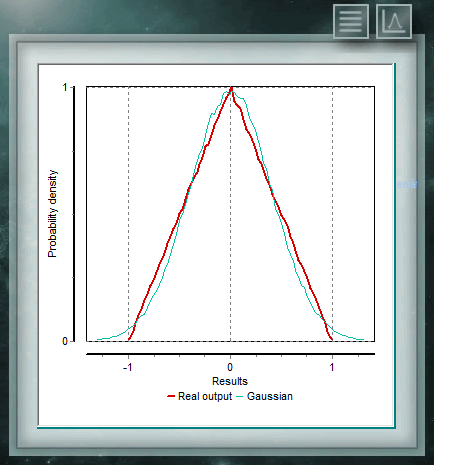 La distribución triangular continua se caracteriza por estar acotada a dos extermos como en el caso de la rectangular, pero además tiene una moda (o valor más probabe) dentro de ese intervalo. La probabilidad en cualquier subintervalo de igual longitud irá aumentando linealmente hasta la moda y luego descenderá de la misma forma hasta la cota superior. Esta distribución es muy utilizada en variables donde la información es limitada, como en el caso de la uniforme, pero donde se tiene un conocimiento aproximado del valor Modal, es decir, donde, si bien no se conoce el punto exacto de este valor, se tiene información de la region o subintervalo donde encontrarlo.
La distribución triangular continua se caracteriza por estar acotada a dos extermos como en el caso de la rectangular, pero además tiene una moda (o valor más probabe) dentro de ese intervalo. La probabilidad en cualquier subintervalo de igual longitud irá aumentando linealmente hasta la moda y luego descenderá de la misma forma hasta la cota superior. Esta distribución es muy utilizada en variables donde la información es limitada, como en el caso de la uniforme, pero donde se tiene un conocimiento aproximado del valor Modal, es decir, donde, si bien no se conoce el punto exacto de este valor, se tiene información de la region o subintervalo donde encontrarlo.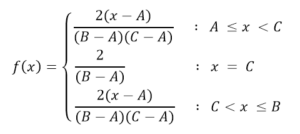
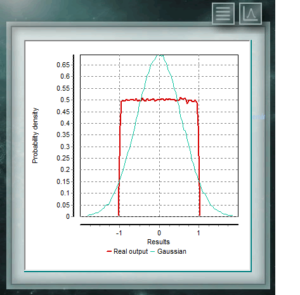 Esta distribución continua se caracteriza por se igualmente probable cualquier valor del intervalo. Es ampliamente utilizada para contribuciones de incertidumbres tipo B en las cuales se conocen únicamente las cotas mayor y menor del intervalo, por ejemplo en la división o resolución de un instrumento digital. En muchos caso tambien puede asignarse esta distribución cuando se tiene poca información sobre la variable aleatoria, en datos de bibliografía o cuando no se conoce el factor de cobertura de una incertidumbre,
Esta distribución continua se caracteriza por se igualmente probable cualquier valor del intervalo. Es ampliamente utilizada para contribuciones de incertidumbres tipo B en las cuales se conocen únicamente las cotas mayor y menor del intervalo, por ejemplo en la división o resolución de un instrumento digital. En muchos caso tambien puede asignarse esta distribución cuando se tiene poca información sobre la variable aleatoria, en datos de bibliografía o cuando no se conoce el factor de cobertura de una incertidumbre,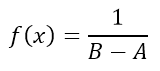
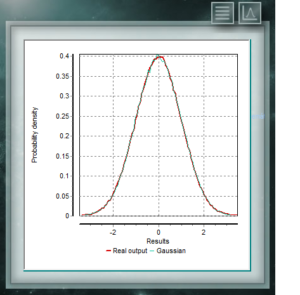 Esta distribución es la que más frecuentemennte se encuentra representando eventos naturales y sociales. Gran parte de las pruebas de la estadística clásica, así como de la estimación de incertidumbres se apoyan en la suposición que los datos se ajustan a una distribución normal. Desde la perspectiva teórica, el Teorema del Límite Central sostiene que dada una muestra aleatoria de tamaño suficientemente, grande se observará que la distribución de medias sigue una distribución aproximadamente normal. La fórmula general de esta distribución es:
Esta distribución es la que más frecuentemennte se encuentra representando eventos naturales y sociales. Gran parte de las pruebas de la estadística clásica, así como de la estimación de incertidumbres se apoyan en la suposición que los datos se ajustan a una distribución normal. Desde la perspectiva teórica, el Teorema del Límite Central sostiene que dada una muestra aleatoria de tamaño suficientemente, grande se observará que la distribución de medias sigue una distribución aproximadamente normal. La fórmula general de esta distribución es: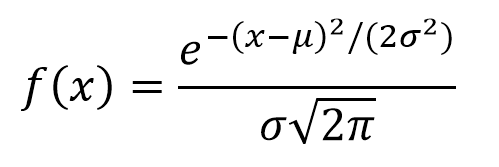
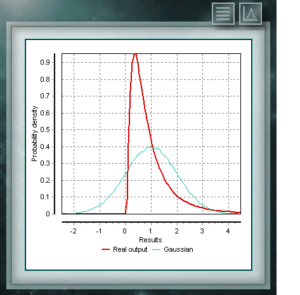 Esta distribución representa a variables aleatorias cuyos logaritmos estan distribuídos de acuerdo a una distribución normal. La distribución lognormal toma diferentes formas según sea el valor de su parámetro de escala y es de uso frecuente en fiabilidad de productos de alta tecnología y también en conteos microbiológicos ya que se basa en el modelo de crecimiento multiplicativo.
Esta distribución representa a variables aleatorias cuyos logaritmos estan distribuídos de acuerdo a una distribución normal. La distribución lognormal toma diferentes formas según sea el valor de su parámetro de escala y es de uso frecuente en fiabilidad de productos de alta tecnología y también en conteos microbiológicos ya que se basa en el modelo de crecimiento multiplicativo.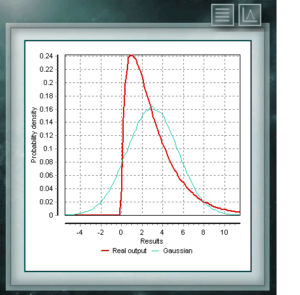 Esta distribución de probabilidad continua en el campo de los reales positivos, está íntimamente relacionada con la distribución Normal, por ejemplo, es la distribución muestral de σ². La distribución Xi (o Chi) Cuadrado queda definida con un único parámetro que son los grados de libertad. La función siempre es asimétrica y sesgada a la derecha. Esta distribución se utiliza muy frecuentemente en diversas ramas de la ciencia ya que permite analizar conjuntos de datos y determinar si la diferencia entre ellos es debida al azar (hipótesis nula) o a otro factor externo.
Esta distribución de probabilidad continua en el campo de los reales positivos, está íntimamente relacionada con la distribución Normal, por ejemplo, es la distribución muestral de σ². La distribución Xi (o Chi) Cuadrado queda definida con un único parámetro que son los grados de libertad. La función siempre es asimétrica y sesgada a la derecha. Esta distribución se utiliza muy frecuentemente en diversas ramas de la ciencia ya que permite analizar conjuntos de datos y determinar si la diferencia entre ellos es debida al azar (hipótesis nula) o a otro factor externo.