Cuando se pulsa el botón de Iniciar simulación, puede verse una barrita bajo el botón que indica en forma continua el avance del muestreo aleatorio. Luego de completar la simulación con los datos indicados, la aplicación se ubica automaticamente en el panel de resultados.

Este panel muestra un selector gráfico arriba a la izquierda, que permite alternar entre los resultados de la simulación de Monte Carlo y el análisis de acuerdo al enfoque GUM, el que también es estimado en todos los casos.

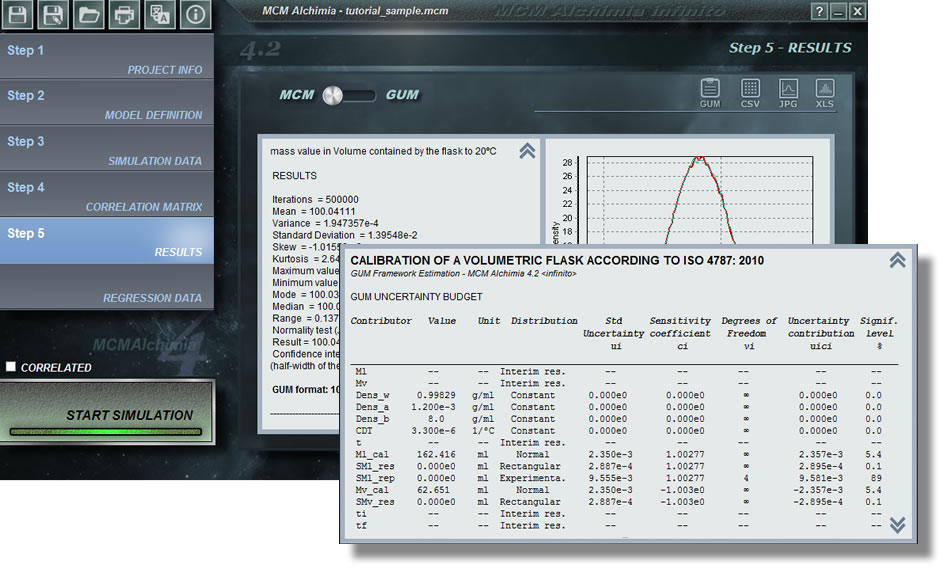
A continuación analizamos la información que brinda la vista de resultados de MCM:

1. Nombre de la aplicación.
2. Versión del software utilizado.
3. Tiempo insumido por la aplicación en la obtención de resultados (en mm.ss, minutos y segundos)
4. Datos técnicos, con el texto que indicamos en el Paso 1
5. Nº de iteraciones. 500 000 en nuestro caso.
6. Análisis estadístico del muestreo
   1. Media = 100.04112
   2. Varianza = 1.99547e-4
   3. Desvío estandar = 1.41335e-2
   4. Skew = -5.43060e-3
   5. Kurtosis = 2.71623
   6. Valor máximo = 100.11225
   7. Valor mínimo = 99.975
   8. Valor más probable = 100.0386
   9. Rango = 0.13726
7. Test de Normalidad (Jarque – Bera) = 1677.68425 (no cumple)
8. Resultado = 100.04111. Esto indica el resultado de la calibración sin redondear cifras.
9. Intervalo de confianza (p = 95,45%): [ 100.01338 , 100.06884 ] (Semi – intervalo = 2.773e-2)
10. Forma clásica: 100.041 ± 0.028 ml. Esto representa el resultado del ensayo y su incertidumbre expandida asociada para la probabilidad de cobertura indicada en el paso 3.
11. Lista de contribuciones a la incertidumbre para cada parámetro del modelo.
12. Sección con datos de entrada y modelo matemático describiendo completamente lo digitado al crear el proyecto de simulación.

Mas ayuda

• Paso 1 – Información del proyecto
• Paso 2-A – Modelo básico.
• Paso 2-B – Incertidumbres de entrada.
• Paso 2-C – Modelo final.
• Paso 3 – Datos de simulación.
• Obtención de los resultados.

Datos de simulación

Lo único que nos resta por hacer en nuestro primer proyecto es asignar una función distribución de probabilidad a cada variable aleatoria que represente nuestro proyecto. Como se ve en el programa, la grilla está compuesta por varias filas, algunas de ellas están con fondo blanco, y otras conn fondo gris. Las filas que tienen fondo gris corresponden a magnitudes para las cuales no puede asignarse una función distribución, debido a que se trata de resultados o resultados intermedios, esto es, magnitudes que se obtendrán en la simulación como resultado de una ecuación secundaria.

La parte inferior del panel de trabajo presenta un cuadro de comandos que nos ofrecerá una lista desplegable de funciones distribución de probabilidad para que nosotros seleccionemos la que se ajusta a la magnitud de entrada. Luego que hayamos seleccionado una FDP, el cuadro inferior nos pedirá que digitemos los parámetros necesarios para realizar la simulación. Por tanto el proceso de este paso sería como sigue:

1. Se recomuenda dejar el número de iteraciones en 500 000 ya que se obtiene in excelente rendimiento en la aplicación y los resultados son absolutamente confiables con este número de iteraciones (puede consultarse el paper: Aspectos computacionales en la estimación de incertidumbres de ensayo por el Método de Monte Carlo)
2. Seleccionamos la probabilidad de cobertura para los resultados. Se recomienda utilizar 95.45% con el fin de obtener resultados para K=2.
3. Hacemos click en la primer fila con fondo blanco (o llegamos a ella con las teclas de cursor de nuestra computadora)
4. Seleccionamos una funcion distribución de probabilidad con la lista desplegable.
5. Llenamos los parámetros de simulación en el panel inferior (tener en cuenta las unidades).
6. Hacemos click en Aplicar. Si todo es correcto, la fila quedará con fondo verde indicando que la magnitud tiene sus datos de simulación correctamente asignados.

Llendo entonces a nuestro matraz aforado tendremos que:

1. V20 : Innhabilitado por ser Resultado, no es posible asignarle una FDP (Función Distribución de Probabilidad)
2. Ml : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
3. Mv : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
4. Dens_w : Asignaremos la PDF Constante de Valor = 0.99829 (g/ml)
5. Dens_a : Asignaremos la PDF Constante de Valor = 1,2E-3 (g/ml)
6. Dens_b : Asignaremos la PDF Constante de Valor = 8.000 (g/ml)
7. CDT : Asignaremos la PDF Constante de Valor = 3.3E-6 (1/ºC)
8. t : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
9. Ml_cal : Por provenir de una incertidumbre expandida, asignaremos la PDF Normal con el valor promedio de nuestras lecturas, Media = 162,416, ingresando la info del certificado en «Usar certificado», con la incertidumbre = 0,0047 (g) y k = 2
10. SM_res : Asignaremos una PDF Rectangular, con Media = 0 (correspondiente a todas las variables que se ingresan solo con fines de estimar incertidumbres) y Semiintervalo = 0,0005, esto es, la mitad de la división de la balanza digital.
11. SM_rep : Para la repetibilidad MCM Alchimia infinito, pone a disposición una FDP experimental donde podremos poner directamente los valores medidos y la aplicación se encargará de hacer los cálculos estadísticos necesarios para utilizar esta información por nosotros. Como es solo con fines de incertidumbre habremos de seleccionar «Forzar media = 0». Usaremos la opción «Directa» y haciendo click en el botón Valores ingresaremos las 5 lecturas de nuestro ensayo: 162,384 ; 162,431 ; 162,409 ; 162,417 ; 162,439
12. Mv_cal : Por provenir de una incertidumbre expandida, asignaremos la PDF Normal con media en la lectura de la balanza en oportunidad de pesar el matraz vacío, Media = 62,651, ingresando la info del certificado en «Usar certificado», con la incertidumbre = 0,0047 (g) y k = 2
13. SMv_res : Asignaremos una PDF Rectangular, con Media = 0 y Semiintervalo = 0,0005.
14. ti : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
15. tf : Innhabilitado por ser Resultado intermedio, no es posible asignarle una FDP
16. corr_t : Asignaremos la PDF Constante de Valor = -0.022 (ºC)
17. ti_cal : Por provenir de un certificado de calibración, asignaremos la PDF Normal con el valor de nuestra lectura del termómetro Media = 20,05 . Al mismo tiempo seleccionaremos «Usar certificado» y pondremos la incertidumbre expandida = 0,021 (ºC) y k = 2.
18. Sti_res : Para esta medida utilizamos un termómetro de mercurio en vidrio de división: 0,1ºC, del que podemos estimar  visualmente 1/4 de la división. De acuerdo a esto, asignaremos una distribución Triangular con Media = 0 y semiintervalo = 0.125 (esto es estimación/2)
19. tf_cal : Se da el mismo caso que en ti_cal pero ahora nuestra media será la temperatura final: Media = 20,075, seleccionaremos «Usar certificado» e indicaremos la incertidumbre expandida = 0,021 (ºC) y k = 2.
20. Stf_res : igual que Sti_res, esto es, Triangular con Media = 0 y semiintervalo = 0.125.

Al ingresar datos para la última magnitud se iluminará el botón «Iniciar simulación» por lo que ya podremos correr nuestra simulacion y obtener los resultados. Vemos entonces los resultados luego de la simulación.

Más ayuda

• Paso 1 – Información del proyecto
• Paso 2-A – Modelo básico.
• Paso 2-B – Incertidumbres de entrada.
• Paso 2-C – Modelo final.
• Paso 3 – Datos de simulación.
• Obtención de los resultados.

Determinación del modelo matemático final para el ensayo.

En el punto anterior vimos que nuestro ensayo de calibración de matraz podria representarse por el diagrama siguiente;

Desglosando las magnitudes de entrada en sus contribuciones nos quedarían entonces:

• Ml = Ml_cal + SMl_res + SMl_rep, donde los sufijos «cal», «res» y «rep» serán por calibración, resolución del instrumento y repetibilidad respectivamente. Los prefijos «S» indican que esta componente tendrá valor cero ya que se agrega solo con fines de estimación de incertidumbres.
• Mv = Mv_cal + SMv_res
• La temperatura dijimos antes que se obtendrá de un promedio, por lo que podemos desgosar la ecuación en este promedio de lecturas. Por otra parte, este termómetro tiene correcciones, podriamos agregar este valor de corrección (corr_t) al promedio como valor constante sin incertidumbre, ya que ésta quedará asociada a los valores originales de temperatura leída.
  t=(ti + tf)/2 + corr_t
• pero cada uno de estos valores estarán afectados por la calibración y la resolución del termómetro. Entonces:
  ti=ti_cal + Sti_res
  tf=tf_cal + Stf_res

Por tanto para concluir este paso 2:

1. Escribimos el modelo completo en el área de texto para el Set de ecuaciones:
   V20=((Ml-Mv)/(Dens_w-Dens_a))*(1-(Dens_a/Dens_b))*(1-CDT*(t-20))
   Ml=Ml_cal+SMl_res+SMl_rep
   Mv=Mv_cal+SMv_res
   t=(ti+tf)/2+corr_t
   ti=ti_cal+Sti_res
   tf=tf_cal+Stf_res
2. Llenamos la grilla de parámetros (inferior) con los siguientes datos:

Más ayuda

• Paso 1 – Información del proyecto
• Paso 2-A – Modelo básico.
• Paso 2-B – Incertidumbres de entrada.
• Paso 2-C – Modelo final.
• Paso 3 – Datos de simulación.
• Obtención de los resultados.

Análisis de las magnitudes de entrada y sus incertidumbres

En esta etapa es recomendable analizar las magnitudes que componen el modelo de entrada para determinar las contribuciones de incertidumbre que aportan. Lo recomendable en este caso es definir un modelo que represente lo más fielmente posible el desarrollo de nuestro análisis o ensayo, de manera que los aportes de incertidumbre se ajusten a los que realmente representarán el modelo.  Si bien nosotros a continuación propondremos una forma de realizarlo, se entiende que cada experto lo realizará a su manera y, por tanto, los diferentes procesos supondran diferentes modelos matemáticos finales para el ensayo. No es el cometido de esta ayuda la discusión de fondo sobre metrología de volumen, sino que, dado un modelo de ensayo encontrar una forma de representarlo fielmente.

Supondremos entonces, para nuestro análisis, que las características del ensayo serán:

• El matraz inicialmente se lava, se seca en estufa, se deja enfriar y se pesa una única vez a 20 ºC en una balanza digital. Esta magnitud, entonces, supondrá contribuciones de incertidumbre por la calibración de la balanza
• La masa del matraz lleno con agua se determinará repitiendo 5 veces la medida, pesanndo en una balanza calibrada. Por tanto esta magnitud aportará incertidumbre por la calibración de la balanza, la resolución de la misma y por la repetibilidad de la medida.
• La temperatura del agua de ensayo se tomará al inicio y al final del ensayo con un termómetro de mercurio en vidrio, utilizándose para el cálculo, el promedio de estas dos medidas. Las contribuciones seran entonces por la calibración del termómetro, la división del mismo y por la deriva encontrada en la medida a lo largo del ensayo.
• Las demás magnitudes (densidades y coeficiente de expansión) se tomarán de tablas y se supondrán constantes en esta oportunidad (sin aporte de incertidumbre)

El diagrama Causa-Efecto (Ishikawa) para nuestro ensayo será entonces:

Para esctibir el modelo completo, entonces se debería desglosar las magnitudes básicas en sus contribuyentes, agregando nuevas lineas al modelo. Esto se discutirá en la siguiente etapa pinchando este enlace.

Más ayuda

• Paso 1 – Información del proyecto
• Paso 2-A – Modelo básico.
• Paso 2-B – Incertidumbres de entrada.
• Paso 2-C – Modelo final.
• Paso 3 – Datos de simulación.
• Obtención de los resultados.