Треугольное распределение
 Непрерывное треугольное распределение характеризуется ограничением до двух крайностей, как в случае прямоугольника, но также имеет режим (или значение более вероятного) в этом диапазоне. Вероятность в любом подинтервале равной длины будет линейно увеличиваться до моды, а затем сходится точно так же, как и к верхней границе. Это распределение широко используется в переменных, где информация ограничена, как в случае однородности, но где мы имеем приблизительное знание Модального значения, то есть, где, хотя точная точка этого значения неизвестна, имеется информация региона или интервала, где его можно найти.
Непрерывное треугольное распределение характеризуется ограничением до двух крайностей, как в случае прямоугольника, но также имеет режим (или значение более вероятного) в этом диапазоне. Вероятность в любом подинтервале равной длины будет линейно увеличиваться до моды, а затем сходится точно так же, как и к верхней границе. Это распределение широко используется в переменных, где информация ограничена, как в случае однородности, но где мы имеем приблизительное знание Модального значения, то есть, где, хотя точная точка этого значения неизвестна, имеется информация региона или интервала, где его можно найти.
Важно: . В случае MCM Alchimmia доступен только треугольный треугольник, то есть статистический режим соответствует среднему значению AB-интервала.
Тогда общее уравнение будет определено для интервала АВ, а вне этих крайностей функция распределения будет равна 0. Формула будет тогда:
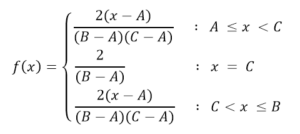
Входные параметры:
- Среднее. Среднее значение и модальное значение случайной величины.
- Полуинтервал. Соответствует середине интервала, к которому применяется это распределение, то есть (B-A) / 2, где A и B — верхняя и нижняя границы интервала. Когда эта функция применяется к неопределенности с помощью разрешения аналогового прибора, этот параметр будет соответствовать оценке (или оценке). Также в области химии обычно допускается перенос объемного материала или даже эталонных материалов в качестве факторов неопределенности распределения треугольников (EURACHEM / QUAM: 2012 8.1.6). В обоих указанных случаях полуинтервал будет соответствовать значению и допустимости материала.
Дополнительная помощь

