Распределение учеников

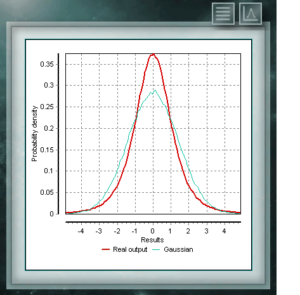Обычно во всех типах анализов, тестов или калибровок предполагается, что повторяющиеся события без внешних стимулов, которые изменяют их вероятности, будут распределяться в соответствии с нормальным или гауссовым распределением, определяемым средним и стандартное отклонение, рассчитанное для образца. Строго говоря, это верно только тогда, когда число повторений велико, согласуется с центральной предельной теоремой, однако, когда у нас недостаточно информации для описания свойств этого гауссовского распределения, потому что наш образец исследования недостаточно велик, предположим, что эти условия также выполняются, мы, несомненно, будем забрасывать значения неопределенности, недооцененные для нашего измерения, как указано в руководстве JCGM 100 — Руководство по выражению неопределенности в измерении.

Эта же проблема была поднята Уильямом Госсетом, который подписал его работу как «Студент» по причинам деловой конфиденциальности компании, в которой он работал. Gosset необходимо было оценить, по экспериментальным данным, распределение, которое представляло небольшие образцы неизвестной дисперсии. Эта функция распределения, предложенная Госсетом, известна как распределение Стьюдента t и отвечает на следующее общее уравнение:

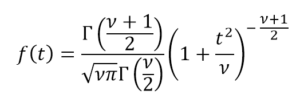
В любой нормально распределенной популяции распределение Стьюдента t позволяет увеличить ширину полученного нормального распределения, чтобы увеличить неопределенность, связанную с измеряемой величиной, в результате бедности информации, предоставленной небольшой выборкой по общей сумме. В той степени, в которой этот образец больше, распределение t будет приближаться к Нормалу, полученному из стандартного отклонения образца, до тех пор, пока оно не будет идентично этому последнему для бесконечных повторений события.

Правильная вещь во всех типах анализа состоит в том, чтобы назначать повторяющимся событиям распределение t с параметром gl, которые будут степенями свободы, значением которых будет количество повторений минус 1. MCM Alchimia позволяет моделировать случайную выборку в соответствии с с распределением Student t не только с этим параметром формы (степенями свободы), но и с параметрами масштаба и положения, через стандартное отклонение и среднее значение соответственно, так что оно может использоваться в любой ситуации, когда это необходимо, без дополнительные операции.

Входные параметры:

• Среднее значение. Этот параметр определяет смещение функции по оси абсцисс. Соответствует среднему значению или среднему значению случайной величины. Поэтому сбор данных этой переменной будет распределен по обеим сторонам этой функции. В случае этого распределения, как и во всех симметричных функциях, среднее будет совпадать со статистическим режимом.
• Степени свободы. Соответствует количеству повторений минус 1, представляет количество значений, которое может меняться без изменения значения среднего значения выборки.
• Стандартное отклонение. Измерение дисперсии значений относительно среднего значения выборки. Если это распределение используется для компонент неопределенности типа A (статистический), это значение может быть рассчитано в соответствии с уравнением:
  
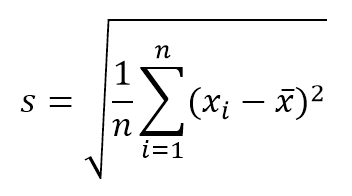
  где n — количество значений или повторений. С другой стороны, если вы хотите знать стандартное отклонение средств выборки, это значение можно получить, разделив s / √ n .