Регрессии и калибровочные кривые

Важно . Эта статья и, следовательно, использование инструмента для кривых MCM Alchimia не учитывает предположений, связанных с применением наименее Квадраты, такие как нормальность, линейность, гомосекустика и независимость. Изучение и валидация этих допущений позволяет нам узнать качество и применимость линейного представления от входных данных, однако MCM Alchimia позволяет подключать кривые, построенные из любого набора входных данных, выполняющего незапланированные наименьшие квадраты, и не обеспечивает или не контролирует соответствие эти предположения.

Обычно можно найти испытания, аналитические методы или калибровки, которые основаны на измерении на разных уровнях аналита или в разных положениях шкалы считывания, когда это инструмент. Таким образом, в большинстве случаев рассматривается линейная связь между ними, получая методом наименьших квадратов коэффициенты уравнения линии:

Таким образом, когда дело доходит до калибровки оборудования, и коррекция строится по шкале считывания, легко получить это значение, применив вышеприведенное уравнение из коэффициентов, полученных наименьшими квадратами и показаниями.

Но обычно особенно в области химии можно построить калибровочную кривую с сертифицированными справочными материалами известной концентрации, а затем использовать эту кривую для получения концентрации аналита от наблюдаемого отклика.

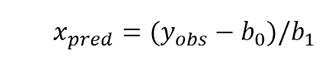
В анализе наименьших квадратов мы имеем три типа неопределенности, связанных с кривой.

• Случайные ошибки в ссылочных ответах y_i .
• Случайные эффекты для ссылочных значений x_i .
• Эффект, связанный с презумпцией линейности, которая будет передаваться отходами.

Если значения x_i и y_i они не представляют неопределенности, полученная кривая будет минимизировать квадраты отходов. В случае случайных ошибок в ссылочных значениях x_i и y_i больше нуля, можно генерировать псевдо-рандомизации с распределением, связанным с каждым параметром, получая по методу наименьших квадратов кривую для каждого набора данных. Это порождает дополнительную неопределенность в коэффициентах регрессии в дополнение к неопределенности, определяемой остатками.

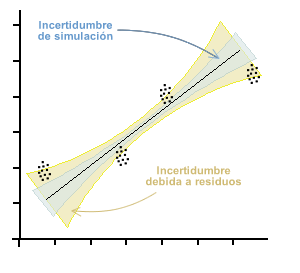
На приведенном ниже графике символически представлен пучок точек, которые каждое наблюдение будет представлять, если имеется значительная неопределенность в обеих осях. Поэтому эта ситуация дает пучок кривых, которые удовлетворяют наименьшим квадратам остатков, порождая неопределенность в обоих коэффициентах регрессии. Эта неопределенность отмечена синим цветом на графике.

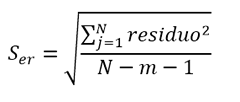
Кроме того, эта неопределенность будет увеличена неопределенностью, присущей кривой, которая определяется как функция стандартного отклонения остаточных ошибок. Эта неопределенность, в общем, больше, чем у моделирования, и представлена ​​оранжевой зоной на графике.

Что делает MCM Alchimia при подключении кривой?

После того, как все значения введены в панель, чтобы использовать кривую в нашей модели, мы должны «соединить» кривую с кнопкой, предусмотренной для этой цели. Когда мы это делаем, MCM Alchimia выполняет симуляцию с набором данных, выполняя произвольную выборку с входными данными и ответом. Для каждой итерации получаются коэффициенты регрессии b₀ и b₁ и значение коэффициента определения R² .

Как и в традиционном моделировании, получается совокупность данных для этих параметров с неизвестным распределением и будет зависеть от распределений и значений входных данных.

Чтобы не делать предположений или неадекватных приближений об этих статистических свойствах, MCM Alchimia сохраняет набор значений в векторах, связанных с этими случайными величинами, которые будут доступны на протяжении всего процесса.

С другой стороны, при средних значениях каждой пары входных данных приложение вычисляет неопределенность кривой в зависимости от остатков регрессии.

Этот репозиторий данных выборки будет использоваться в соответствии с потребностью нашей модели либо с использованием их коэффициентов b₀, либо b₁ с учетом их неопределенности, чтобы рассмотреть неопределенность кривая или использовать функции интерполяции, которые будут описаны ниже.