Нормальное распределение (гауссовское)
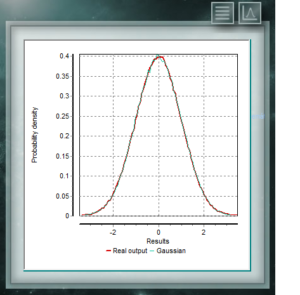 Это распределение является тем, которое чаще всего представляет собой природные и социальные события. Значительная часть доказательств классической статистики, а также оценка неопределенностей основаны на предположении, что данные соответствуют нормальному распределению. С теоретической точки зрения Центральная предельная теорема утверждает, что, учитывая случайную выборку достаточно больших размеров, будет наблюдаться, что распределение сред следует приблизительно нормальному распределению. Общая формула этого распределения:
Это распределение является тем, которое чаще всего представляет собой природные и социальные события. Значительная часть доказательств классической статистики, а также оценка неопределенностей основаны на предположении, что данные соответствуют нормальному распределению. С теоретической точки зрения Центральная предельная теорема утверждает, что, учитывая случайную выборку достаточно больших размеров, будет наблюдаться, что распределение сред следует приблизительно нормальному распределению. Общая формула этого распределения:
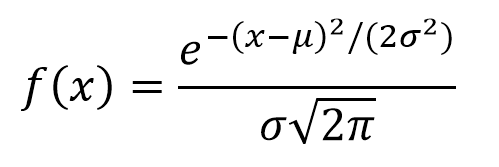
где μ обозначает местоположение и σ масштаб функции. Чтобы оценить неопределенность измерения, μ соответствует среднему значению и значению режима случайной величины, а σ — стандартное отклонение.
Входные параметры:
- Значение. Среднее значение или среднее значение случайной величины. Поэтому сбор данных этой переменной будет распределен по обеим сторонам этой функции. В случае этого нормального или гауссовского распределения среднее будет совпадать со способом.
- Стандартное отклонение. Измерение дисперсии значений относительно среднего значения выборки. Если это распределение используется для компонент неопределенности типа A (статистический), это значение может быть рассчитано в соответствии с уравнением:
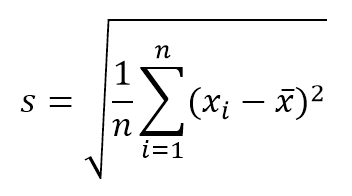
где n — количество значений или повторений. С другой стороны, если вы хотите знать стандартное отклонение среднего значения выборки, это значение можно получить, разделив s / √ n .
Если параметр, которому присвоено это распределение, соответствует вкладу неопределенности в сертификате калибровки, стандартное отклонение соответствует стандартной неопределенности ( u ) или расширенной неопределенности, деленной на коэффициент покрытия k.
Дополнительная помощь

