La distribución t Student

Desde hace décadas es usual suponer en todo tipo de análisis, ensayos o calibraciónes que los eventos repetitivos, sin estímulos externos que varíen sus probabilidades, se distribuirán de acuerdo a una distribución Normal o Gaussiana definida por la media y la desvíación estándar calculada en la muestra. En rigor esto solamente es cierto cuando el número de repeticiones es grande, gracias al teorema central del límite, sin embargo cuando no tenemos suficiente información para describir las propiedades de esta Normal debido a que nuestra muestra en estudio no es lo suficientemente grande, suponer que se cumplen igualmente estas condicione, nos arrojará seguramente valores de incertidumbre subestimados para nuestro mesurand .o, gomo lo indica la guía JCGM 100 – Guide to the expression of uncertainty in measurement.

Este mismo problema se lo planteó William Gosset, quien firmaba sus trabajos como Student por razones de confidencialidad empresarial de la compañía donde trabajaba. Gosset necesitaba estimar a partir de datos experimentales, una distribución que representara muestraa pequeñas de varianza desconocida. Esta función distribución propuesta por Gosset se conoce como t Student, y responde a la ecuación general siguiente:

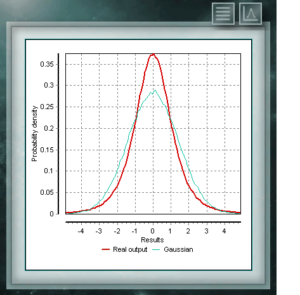
En toda población normalmente distribuída, la distribución t Student permite incrementar el ancho de la distribución normal resultante para incrementar la incertidumbre asociada al mesurando como resultado de la pobreza de información que aporta una muestra pequeña sobre el lote total. En la medida que esta muestra sea mayor, la distribución t se irá acercando a la Normal obtenida a partir del desvio estandar de la muestra hasta ser identica a esta última para infinitas repeticiones del evento.

Lo correcto entonces en todo tipo de análisis es asignar a eventos repetitivos la distribución t con un parámetro gl que serán los grados de libertad, cuyo valor será la cantidad de repeticiones menos 1. MCM Alchimia infinito permite simular la distribución t Student, no solo con este parámetro de forma, sinó con parámetros de escala y de posición, a traves del desvío estandar y la media respectivamente, para que pueda utilizarse en cualquier situación donde corresponda, sin operaciones adicionales.

Parametros de entrada:

• Media. Este parámetro define el desplazamiento de la función en el eje de abscisas. Corresponde al valor medio, o promedio de la variable aleatoria. La colección de datos de esta variable, por tanto, se distribuirán a ambos lados de esta función. En el caso de esta distribución, al igual que en todas las funciones simétricas la media coincidirá con la moda.
• Grados de libertad. Corresponde al número de repeticiones menos 1, Representa el numero de valores que pueden variar sin modificar el valor de la media muestral.
• Desvío estandar. Medida de la dispersión de los valores respecto de la media muestral. Si se utiliza esta distribución para componentes de incertidumbre Tipo A (estadísticos), este valor puede calcularse según la ecuación:
  
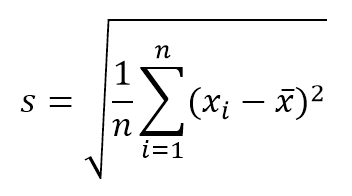
  donde n es el número de valores o repeticiones. Por otra parte, si lo que se desea conocer es el desvío estándar de las medias muestrales, este valor puede obtenerse dividiendo s/√n.