Distribución Normal (Gaussiana)

by admin

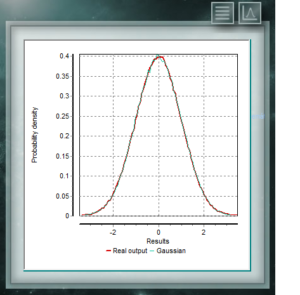Esta distribución es la que más frecuentemennte se encuentra representando eventos naturales y sociales.  Gran parte de las pruebas de la estadística clásica, así como de la estimación de incertidumbres se apoyan en la suposición que los datos se ajustan a una distribución normal. Desde la perspectiva teórica, el Teorema del Límite Central sostiene que dada una muestra aleatoria de tamaño suficientemente, grande se observará que la distribución de medias sigue una distribución aproximadamente normal. La fórmula general de esta distribución es:

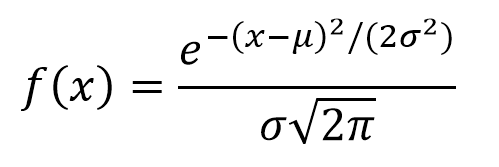
donde μ representa la localización y σ la escala de la función.  Con el fin de estimar incertidumbres de ensayo, μ corresponde al valor medio y moda de la variable aleatoria, mientras que σ es el desvío estándar.

Parametros de entrada:

  • Media. Valor medio, o promedio de la variable aleatoria. La colección de datos de esta variable, por tanto, se distribuirán a ambos lados de esta función. En el caso de esta distribución Normal o Gaussiana, la media coincidirá con la moda.
  • Desvío estandar. Medida de la dispersión de los valores respecto de la media muestral. Si se utiliza esta distribución para componentes de incertidumbre Tipo A (estadísticos), este valor puede calcularse según la ecuación:

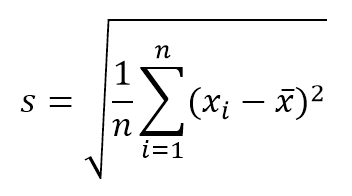
    donde n es el número de valores o repeticiones. Por otra parte, si lo que se desea conocer es el desvío estándar de las medias muestrales, este valor puede obtenerse dividiendo s/√n.

Si el parámetro al que se asigna esta distribución corresponde al aporte de incertidumbre proveniente de un certificado de calibración, el desvío estandar corresponde a la incertidumbre estandar (u), o a la incertidumbre expandida dividido el factor de cobertura.

Más ayuda