Dreieckige Verteilung
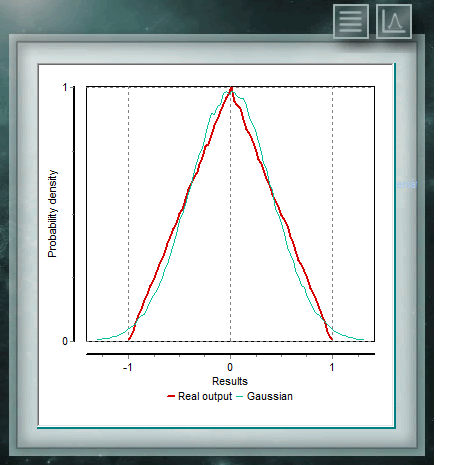 Die durchgehende Dreiecksverteilung ist dadurch gekennzeichnet, dass sie wie im Fall des Rechtecks an zwei Extreme begrenzt ist, aber auch einen Modus (oder einen wahrscheinlicheren Wert) innerhalb dieses Bereichs aufweist. Die Wahrscheinlichkeit in jedem Teilintervall gleicher Länge steigt linear bis zur Art und Weise und fällt dann auf die gleiche Weise bis zur oberen Grenze ab. Diese Verteilung wird häufig in Variablen verwendet, bei denen die Informationen begrenzt sind, wie im Fall der Uniform, bei denen jedoch eine ungefähre Kenntnis des Modalwerts vorliegt, d. H. Wo der genaue Punkt dieses Wertes nicht bekannt ist, jedoch Informationen vorhanden sind der Region oder des Teilintervalls, wo sie zu finden sind.
Die durchgehende Dreiecksverteilung ist dadurch gekennzeichnet, dass sie wie im Fall des Rechtecks an zwei Extreme begrenzt ist, aber auch einen Modus (oder einen wahrscheinlicheren Wert) innerhalb dieses Bereichs aufweist. Die Wahrscheinlichkeit in jedem Teilintervall gleicher Länge steigt linear bis zur Art und Weise und fällt dann auf die gleiche Weise bis zur oberen Grenze ab. Diese Verteilung wird häufig in Variablen verwendet, bei denen die Informationen begrenzt sind, wie im Fall der Uniform, bei denen jedoch eine ungefähre Kenntnis des Modalwerts vorliegt, d. H. Wo der genaue Punkt dieses Wertes nicht bekannt ist, jedoch Informationen vorhanden sind der Region oder des Teilintervalls, wo sie zu finden sind.
Wichtig: Bei MCM Alchimmia ist nur das zentrierte Dreieck verfügbar, dh der statistische Modus entspricht dem Durchschnittswert des AB-Intervalls.
Die allgemeine Gleichung wird dann für das Intervall AB definiert, während außerhalb dieser Extremwerte die Verteilungsfunktion 0 ist. Die Formel lautet dann:
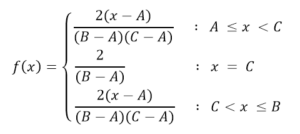
Eingabeparameter:
- Durchschnitt. Mittelwert und Modalwert der Zufallsvariablen.
- Halbintervall. Entspricht der Mitte des Intervalls, auf das diese Verteilung angewendet wird, dh (B-A) / 2, wobei A und B die oberen und unteren Grenzen des Intervalls sind. Wenn diese Funktion durch Auflösung eines Analoginstruments auf die Unsicherheit angewendet wird, entspricht dieser Parameter der Aufwertung (oder Schätzung & lt; e & gt;). Auch auf dem Gebiet der Chemie ist es üblich, die Toleranz des volumetrischen Materials oder sogar der Referenzmaterialien als Ursache für die Unsicherheit der Dreieckverteilung zu betrachten (EURACHEM / QUAM: 2012 8.1.6). In beiden Fällen entspricht das Halbintervall dem Wert und der Toleranz des Materials.
Mehr Hilfe

