Normalverteilung (Gaussian)
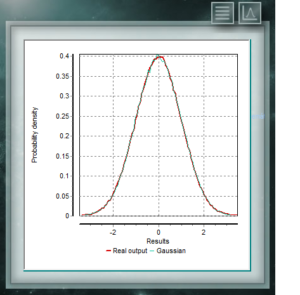 Diese Verteilung ist diejenige, die am häufigsten natürliche und soziale Ereignisse darstellt. Die meisten Beweise aus der klassischen Statistik sowie die Abschätzung von Unsicherheiten beruhen auf der Annahme, dass die Daten einer Normalverteilung entsprechen. Aus theoretischer Sicht behauptet der zentrale Grenzwertsatz, dass bei einer ausreichend großen Stichprobe die Verteilung der Mittel einer annähernd Normalverteilung folgt. Die allgemeine Formel dieser Verteilung lautet:
Diese Verteilung ist diejenige, die am häufigsten natürliche und soziale Ereignisse darstellt. Die meisten Beweise aus der klassischen Statistik sowie die Abschätzung von Unsicherheiten beruhen auf der Annahme, dass die Daten einer Normalverteilung entsprechen. Aus theoretischer Sicht behauptet der zentrale Grenzwertsatz, dass bei einer ausreichend großen Stichprobe die Verteilung der Mittel einer annähernd Normalverteilung folgt. Die allgemeine Formel dieser Verteilung lautet:
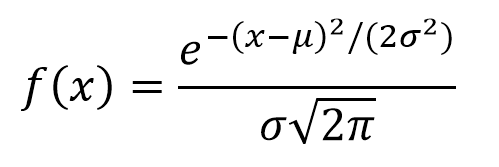
wobei μ den Ort und σ die Skala der Funktion darstellt. Um eine Messunsicherheit abzuschätzen, entspricht µ dem Mittelwert und dem Moduswert der Zufallsvariablen, während σ die Standardabweichung ist.
Eingabeparameter:
- Mittelwert Durchschnittswert oder Durchschnitt der Zufallsvariablen. Die Datensammlung dieser Variablen wird daher auf beiden Seiten dieser Funktion verteilt. Bei dieser Normal- oder Gaußschen Verteilung stimmt der Mittelwert mit der Mode überein.
- Standardabweichung. Maß der Streuung der Werte in Bezug auf den Mittelwert der Probe. Wenn diese Verteilung für (statistische) Unsicherheitskomponenten vom Typ A verwendet wird, kann dieser Wert gemäß der folgenden Gleichung berechnet werden:
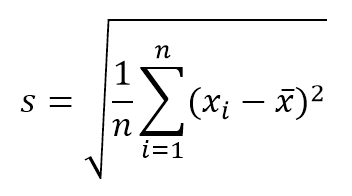
Dabei ist n die Anzahl der Werte oder Wiederholungen. Wenn Sie dagegen die Standardabweichung des Mittelwerts der Stichprobe wissen möchten, können Sie diesen Wert erhalten, indem Sie s / √ n teilen.
Wenn der Parameter, dem diese Verteilung zugeordnet ist, dem Unsicherheitsbeitrag eines Kalibrierungszertifikats entspricht, entspricht die Standardabweichung der Standardunsicherheit ( u ) oder der erweiterten Unsicherheit dividiert durch den Überdeckungsfaktor k.
Mehr Hilfe

