Lognormalverteilung
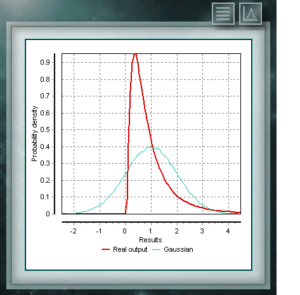 Diese Verteilung stellt Zufallsvariablen dar, deren Logarithmen gemäß einer Normalverteilung verteilt sind. Die logarithmische Normalverteilung nimmt abhängig vom Wert ihres Skalenparameters unterschiedliche Formen an und wird häufig in der Zuverlässigkeit von Hochtechnologieprodukten und auch in mikrobiologischen Zählungen verwendet, da sie auf dem multiplikativen Wachstumsmodell basieren.
Diese Verteilung stellt Zufallsvariablen dar, deren Logarithmen gemäß einer Normalverteilung verteilt sind. Die logarithmische Normalverteilung nimmt abhängig vom Wert ihres Skalenparameters unterschiedliche Formen an und wird häufig in der Zuverlässigkeit von Hochtechnologieprodukten und auch in mikrobiologischen Zählungen verwendet, da sie auf dem multiplikativen Wachstumsmodell basieren.
Eingabeparameter:
Wie angegeben, werden die Logarithmen der Werte der logarithmischen Zufallsvariablen gemäß einer Gaußschen Funktion verteilt. Diese Verteilungsfunktion kann aus zwei Parametersätzen definiert werden, die in den Optionsfeldern rechts im Datenfeld ausgewählt werden.
- μ (Y). Durchschnittliche Daten der Bevölkerung Y Diese Y-Population wird nach der Gruppe von Daten definiert, auf die wir uns beziehen möchten, dh auf die lognormale Population oder die normale Population ihrer Logarithmen.
- s (Y). Standardabweichung von Y. Mit Y gemäß den oben angegebenen Eigenschaften.
- Y = X (LogNormal) / Y = In (X) (Normal). Mit diesem Selektor können Sie auswählen, auf welche Datengruppe sich die Eingabeparameter beziehen.
- Y = X (LogNormal). In diesem ersten Fall bilden die generierten Pseudozufallszahlen eine lognormale Verteilung, deren Mittelwert μ (Y) ist, und ihre Standardabweichung ist s (Y).
- Y = ln (X) (Normal). In diesem Fall werden die generierten Werte in LogNormal-Form verteilt. Der durch die Logarithmen dieser Daten gebildete Satz hat eine Normalverteilung, deren Mittelwert μ (Y) ist, und seine Standardabweichung ist s (Y) .
Mehr Hilfe

