Erstes Projekt – Schritt 3
Simulationsdaten
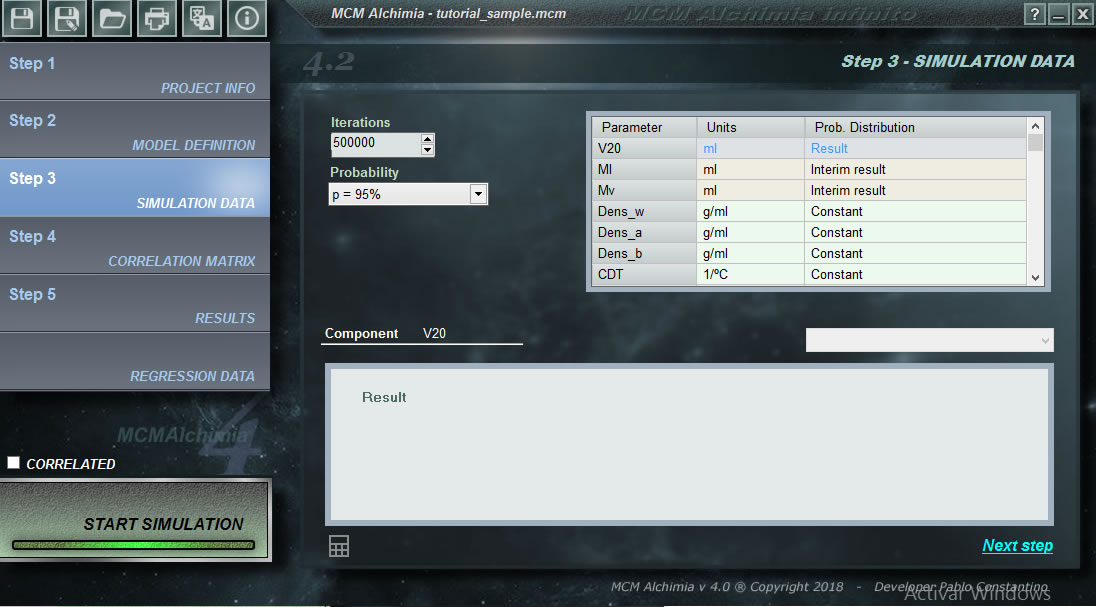
Das erste, was wir in unserem ersten Projekt tun müssen, ist, jeder Zufallsvariablen, die unser Projekt darstellt, eine Wahrscheinlichkeitsverteilungsfunktion zuzuweisen. Wie aus dem Programm ersichtlich, besteht das Raster aus mehreren Zeilen, einige davon mit weißem Hintergrund und andere mit grauem Hintergrund. Die grau hinterlegten Zeilen entsprechen Beträgen, für die keine Verteilungsfunktion zugeordnet werden kann, da es sich um Zwischenergebnisse oder um das Endergebnis handelt, dh um Beträge, die in der Simulation als Ergebnis von Sekundärgleichungen erhalten werden.
Der untere Teil des Arbeitsbereichs verfügt über ein Befehlsfeld, in dem eine Dropdown-Liste mit Wahrscheinlichkeitsverteilungsfunktionen angezeigt wird, sodass wir diejenige auswählen können, die zur Eingabegröße passt. Nachdem wir eine Wahrscheinlichkeitsverteilung ausgewählt haben, werden Sie im unteren Kästchen aufgefordert, die erforderlichen Parameter einzugeben, um die Simulation durchzuführen. Der Prozess dieses Schritts wäre daher wie folgt:
- Es wird empfohlen, die Anzahl der Iterationen auf 500 000 zu belassen, da sie in der Anwendung eine hervorragende Leistung aufweist und die Ergebnisse bei dieser Anzahl von Iterationen absolut zuverlässig sind (siehe das Dokument: Berechnungsaspekte bei der Abschätzung von Testunsicherheiten nach der Monte-Carlo-Methode (nur Spanisch)
- Wir wählen die Deckungswahrscheinlichkeit für die Ergebnisse. Es wird empfohlen, 95,45% zu verwenden, um Ergebnisse für K = 2 zu erhalten.
- Wir klicken auf die erste Zeile mit weißem Hintergrund (oder erreichen sie mit den Cursortasten unserer Tastatur)
- Wir wählen eine Wahrscheinlichkeitsverteilungsfunktion in der Dropdown-Liste aus.
- Wir füllen die Simulationsparameter im unteren Bereich (bitte berücksichtigen Sie die Einheiten).
- Wir klicken auf Übernehmen. Wenn alles korrekt ist, wird die Zeile grün hinterlegt, was darauf hinweist, dass die Simulationsdaten der Größe korrekt zugeordnet sind.
Wenn wir zu unserem Messkolben zurückkehren, werden wir folgendes haben:
- V20 : Deaktiviert, da es sich um ein Ergebnis handelt, , es ist nicht möglich, eine Wahrscheinlichkeitsverteilungsfunktion zuzuordnen
- Ml : Deaktiviert, da es sich um ein Zwischenergebnis handelt, Es ist nicht möglich, eine Wahrscheinlichkeitsverteilung zuzuordnen.
- Mv : Deaktiviert, da es sich um ein Zwischenergebnis handelt, Es ist keine Zuordnung einer Wahrscheinlichkeitsverteilung möglich.
- Dens_w : Wir weisen den Eintrag Konstante mit einem Wert = 0,99829 (g / ml)
- Dens_a : Weisen Sie den Eintrag Konstante mit einem Wert = 1,2E-3 (g / ml)
- Dens_b : Wir weisen den Eintrag Konstante mit einem Wert = 8.000 (g / ml)
- CDT : Weisen Sie den Eintrag Konstante mit Wert = 3.3E-6 (1 / ºC)
- t : Deaktiviert, da es sich um ein Zwischenergebnis handelt, Es ist nicht möglich, eine Wahrscheinlichkeitsverteilung zuzuordnen
- Ml_cal : Aufgrund einer erweiterten Unsicherheit weisen wir die Verteilung Normal mit dem Durchschnittswert unserer Messwerte (Mittelwert = 162,416) zu und geben die Zertifikatinformationen in „Verwendung“ ein Zertifikat „, mit Unsicherheit = 0,0047 (g) und k = 2
- SM_res : Wir weisen eine Rechteckige -Verteilung mit Mean = 0 (entspricht allen Variablen, die nur zum Schätzen von Unsicherheiten eingegeben werden) und einem halben Intervall zu = 0,0005, dh die Hälfte der Einteilung der digitalen Waage.
- SM_rep: : Zur Wiederholbarkeit bietet MCM Alchimia eine experimentelle Verteilung, in der wir die gemessenen Werte direkt eingeben können. Die Anwendung ist dafür verantwortlich, die statistischen Berechnungen vorzunehmen, die für die Simulation erforderlich sind . Da es nur zu Unsicherheitszwecken ist, müssen wir „Durchschnitt = 0“ auswählen. Wir verwenden die Option „Direkt“ und klicken auf die Schaltfläche „Werte“. Wir geben die 5 Lesungen unseres Aufsatzes ein: 162.384; 162,431; 162.409; 162.417; 162.439
- Mv_cal : Aufgrund einer erweiterten Unsicherheit weisen wir die Verteilung Normal mit einem Mittelwert in der Waage auf, um den leeren Kolben zu wiegen, Mean = 62.651, Eingabe der Zertifikatsinformationen in „Zertifikat verwenden“, mit Unsicherheit = 0,0047 (g) und k = 2
- SMv_res : Wir werden eine rechteckige -Distribution mit Media = 0 und Half-Intervall = 0.0005 zuweisen.
- ti : Deaktiviert, da es sich um ein Zwischenergebnis handelt, Es kann keine Verteilung zugewiesen werden
- tf : Deaktiviert, da es sich um ein Zwischenergebnis handelt, Es ist nicht möglich, eine Wahrscheinlichkeitsverteilung zuzuordnen.
- corr_t : Wir weisen den Eintrag Konstante mit Wert = -0.022 (ºC) zu
- ti_cal : Da es aus einem Kalibrierungszertifikat stammt, weisen wir dem PDF-Format Normal den Wert des Durchschnittswerts des Thermometers = 20,05 zu. Gleichzeitig wählen wir „Use certificate“ und setzen die erweiterte Unsicherheit = 0,021 (ºC) und k = 2.
- Sti_res : Für diese Maßnahme verwenden wir ein Quecksilberthermometer im Glas der Division: 0,1 ° C, von dem wir 1/4 der Division visuell abschätzen können. Dementsprechend werden wir eine Dreieckverteilung mit Mean = 0 und Half-Intervall = 0,125 (dies ist Schätzung / 2) zuweisen
- tf_cal : Das Gleiche ist wie in ti_cal, aber jetzt ist der Durchschnitt die Endtemperatur k = 2.
- Stf_res : Wie Sti_res, dh Dreieckig mit Media = 0 und Semi-Intervall = 0,125.
Wenn Sie Daten für die letzte Größe eingeben, leuchtet die Schaltfläche „Simulation ausführen“ auf, sodass wir unsere Simulation ausführen und die Ergebnisse erhalten können. Ergebnisse nach der Simulation ansehen .
Mehr Hilfe

